Ellipse and Circle
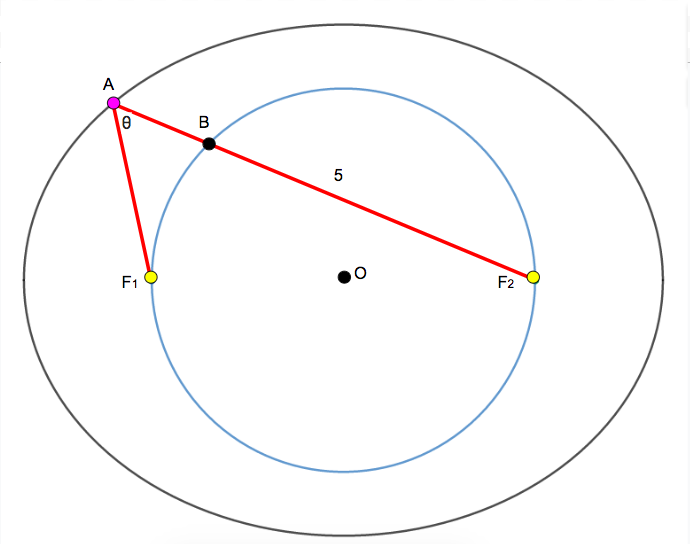
Ellipse A : 1 6 x 2 + 2 5 y 2 = 4 0 0 , centered at O ( 0 , 0 ) , has foci at F 1 and F 2 . Circle O has its diameter ends at F 1 and F 2 as shown in the figure. If B F 2 = 5 and cos ( ∠ F 1 A F 2 ) = n m , where m and n are positive coprime integers, find the value of m + n + m n .
The answer is 151.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
By putting the ellipse in standard form, the semi-minor axis is 4 and the semi-major axis is 5 . The foci are a length of 3 away from the center.
A Triangle can be constructed by connecting the upper endpoint of the semi-minor axis, the right focus, and the center. This results in the length from the upper endpoint of the semi-minor axis to the right focus being 5 because of the Pythagorean theorem as the minor axis and major axis are perpendicular. By doing the same to the other focus, the length from the upper endpoint of the semi-minor axis to the left focus is also 5 . Since the sum of lengths from a point on the ellipse to the two foci are the same, A F 1 + A F 2 = 5 + 5 = 1 0 .
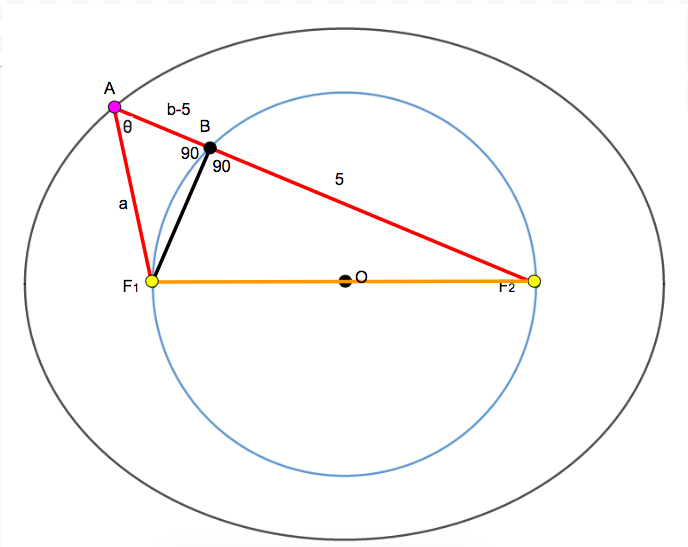
Next, the construction in the following diagram can be drawn. Angle F 1 B F 2 = 9 0 because B F 1 and B F 2 connect the endpoints of a diameter. Let A F 2 = b and A F 1 = a . Then, A B = b − 5 since B F 2 = 5 . Also, F 1 F 2 = 3 + 3 = 6 since the length from one focus to the center is 3 . By the pythagorean theorem, B F 1 = √ 1 1 . Because A F 1 + A F 2 = a + b = 1 0 , the pythagorean theorem can be used again to determine the lengths of a and b since 1 1 + ( b − 5 ) 2 = a 2 = ( 1 0 − b ) 2 . By solving this, b = 6 . 4 , b − 5 = 6 . 4 − 5 = 1 . 4 and a = 3 . 6 . Since A B F 1 is a right triangle, cos ( θ ) = 3 . 6 1 . 4 = 1 8 7 . As a result, m = 7 and n = 1 8 so ( 7 + 1 8 + ( 7 ∗ 1 8 ) ) = 1 5 1 which is the final answer.
From 1 6 x 2 + 2 5 y 2 = 4 0 0 ⟹ 5 2 x 2 + 4 2 y 2 = 1 . Therefore the major and minor semi-axes are a = 5 and b = 4 respectively. Let the distance between the center and a focus be c . Then c = a 2 − b 2 = 5 2 − 4 2 = 3 . Therefore F 1 F 2 = 2 c = 6 .
Since F 1 F 2 is a diameter of circle B , then ∠ F 1 B F 2 = 9 0 ∘ as shown in the figure below.
Let A B = x and A F 1 = y , then cos ( ∠ F 1 A F 2 ) = y x = n m . By the definition of ellipse :
A F 1 + A F 2 5 + x + y ⟹ x + y = 2 a = 1 0 = 1 0 = 5 . . . ( 1 )
By Pythagorean theorem :
A F 1 2 − A B 2 y 2 − x 2 ( y − x ) ( y + x ) ⟹ y − x = F 1 F 2 2 − B F 2 2 = 6 2 − 5 2 = 1 1 = 5 1 1 . . . ( 2 ) Note that ( 1 ) : x + y = 5
From ( 1 ) + ( 2 ) : 2 y = 5 + 5 1 1 ⟹ y = 5 1 8 and x = 5 7 . ⟹ cos ∠ F 1 A F 2 = y x = 1 8 7 . Therefore, m + n + m n = 7 + 1 8 + 7 × 1 8 = 1 5 1 .