Ellipse arrangement in an isosceles triangle
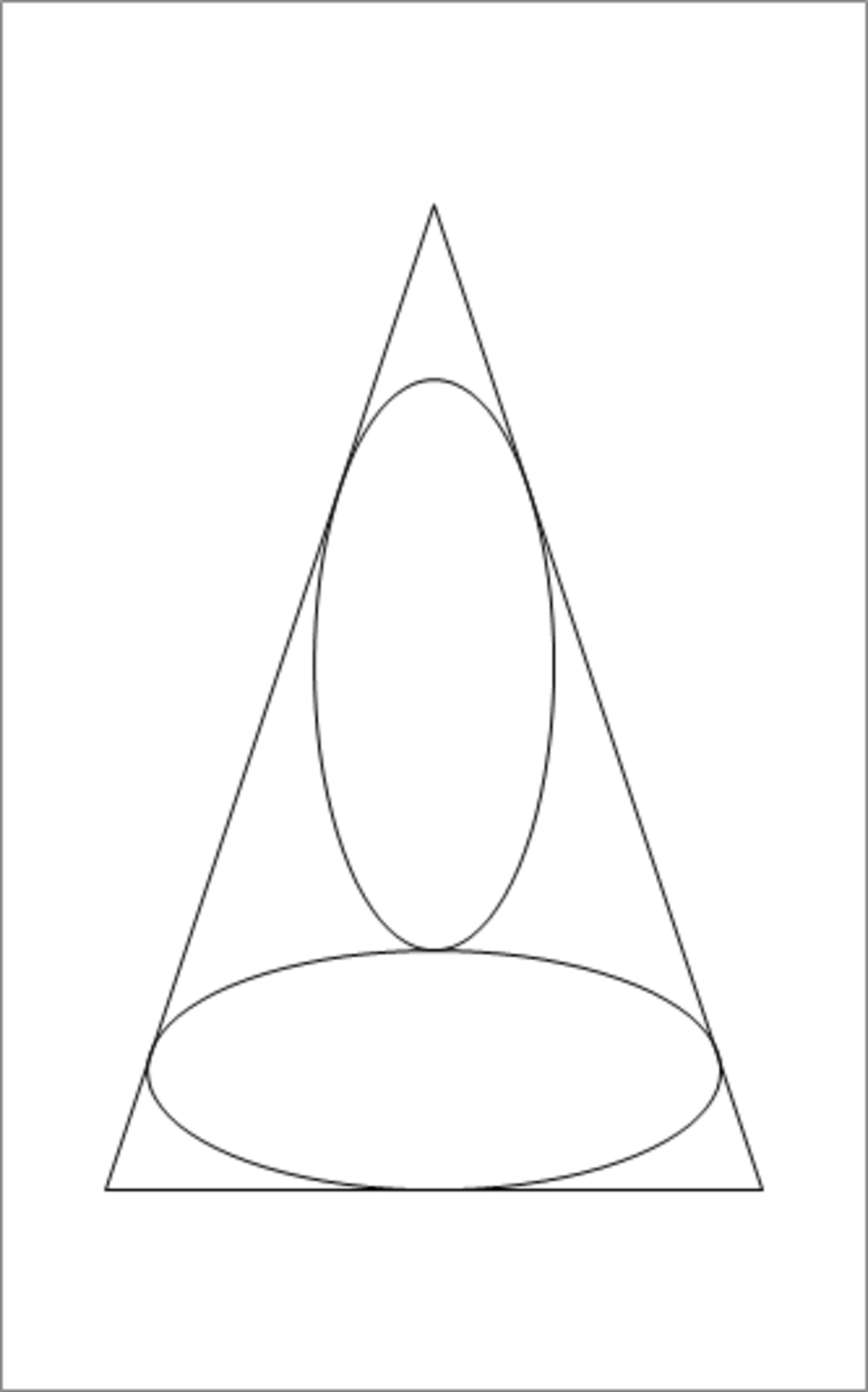
Starting with an isosceles triangle where the altitude is times the base, we inscribe two identical ellipses with their axes parallel to the base and the altitude as shown in the figure above. Find the eccentricity of either of the two ellipses, and enter
The answer is 9074.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the triangle have a base of 2 and an altitude of 3 , and place it on the coordinate plane so that its vertices are at ( ± 1 , 0 ) and ( 0 , 3 ) . Then its congruent sides follow the equations y = ± 3 x + 3 .
Let the ellipses have a semi-major axis of a and a semi-minor axis of b . Then the bottom ellipse has a center of ( 0 , b ) and an equation of a 2 x 2 + b 2 ( y − b ) 2 = 1 , and the top ellipse has a center of ( 0 , a + 2 b ) and an equation of b 2 x 2 + a 2 ( y − a − 2 b ) 2 = 1 .
Since the bottom ellipse is inscribed in the triangle, it will touch one its sides in only one place, so after substituting y = − 3 x + 3 into a 2 x 2 + b 2 ( y − b ) 2 = 1 , the discriminant of x must be 0 ; that is, a b 3 ( 3 a 2 + 2 b − 3 ) = 0 , which solves to b = 2 1 ( 3 − 3 a 2 ) for positive values of a and b .
Similarly, the top ellipse will also touch one of the triangle's sides in only one place, so after substituting y = − 3 x + 3 and b = 2 1 ( 3 − 3 a 2 ) into b 2 x 2 + a 2 ( y − a − 2 b ) 2 = 1 , the discriminant of x must be 0 ; that is, a ( a 2 − 1 ) 3 ( 3 a 2 − 2 a − 3 ) ( 5 a 2 + 6 a − 9 ) = 0 , which solves to a = 5 3 6 − 3 for 0 < a < 1 .
If a = 5 3 6 − 3 , then b = 2 1 ( 3 − 3 a 2 ) = 2 1 ( 3 − 3 ( 5 3 6 − 3 ) 2 ) = 2 5 2 7 6 − 5 7 , and e = a a 2 − b 2 = 5 3 6 − 3 ( 5 3 6 − 3 ) 2 − ( 2 5 2 7 6 − 5 7 ) 2 = 5 2 7 6 − 1 2 ≈ 0 . 9 0 7 4 2
Therefore, ⌊ 1 0 4 e ⌋ = 9 0 7 4 .