Ellipse Butterfly! - Part 1

Geometry Level 5

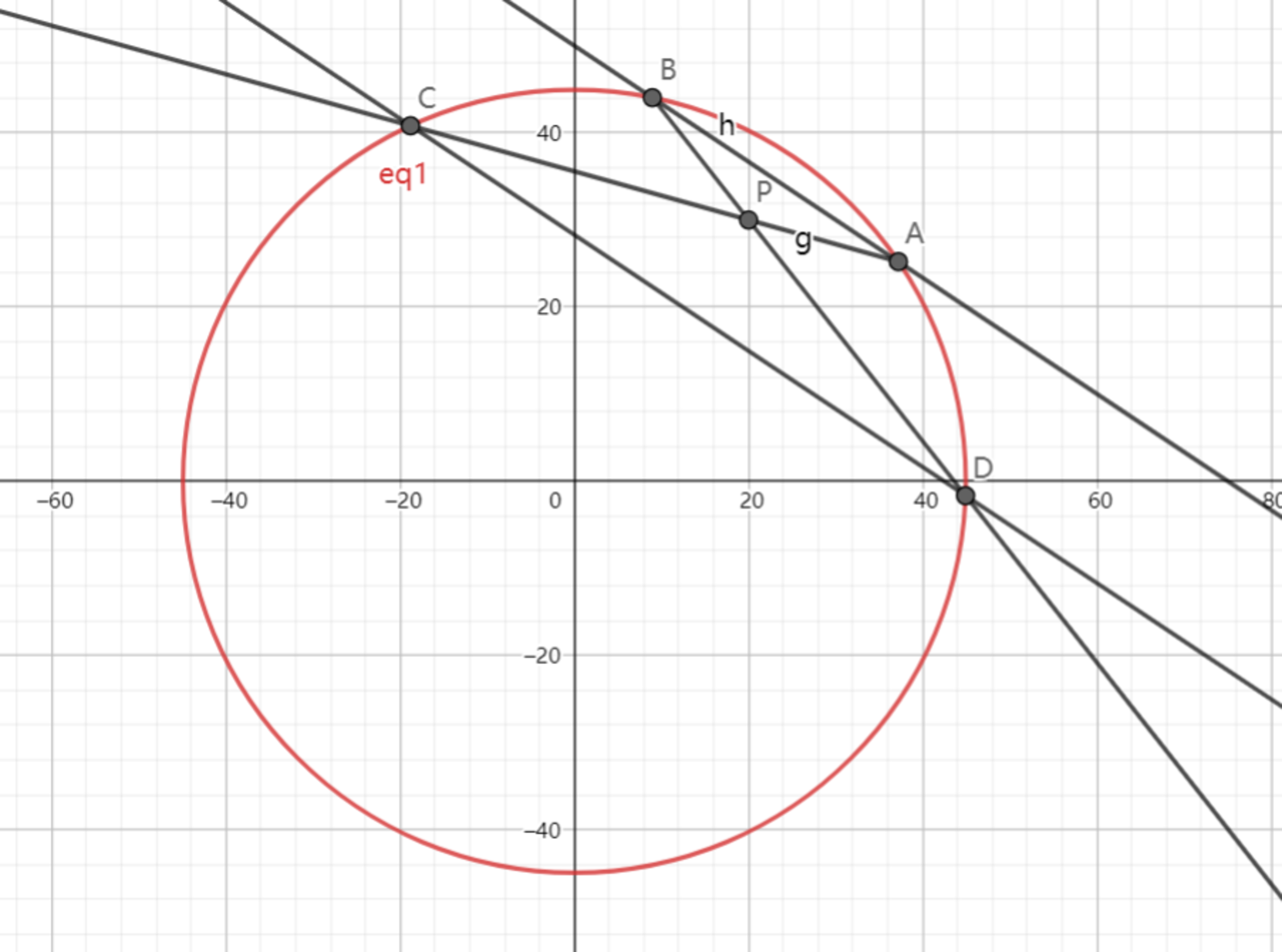
As shown above, the ellipse has equation: $\dfrac{x^2}{2020}+\dfrac{y^2}{2019}=1$ , $P(20,30)$ , $l_1$ intersects with the ellipse at point $A,B$ , $l_2$ intersects with the ellipse at point $C,D$ , and line $AC,BD$ intersect at point $P$ .

Given that $l_1 \parallel l_2$ , find the slope of $l_1, l_2$ .

If the slope is $k$ , and $|k|=\dfrac{p}{q}$ , where $p,q$ are positive coprime integers. Submit $p+q$ .

The answer is 1683.

1 solution

Kris Hauchecorne
Jun 19, 2020

General form of this conic section is:

2019x²+2020y²-4078380=0

Expanding to homogeneous coördinates where finite points get an extra coordinate z=1 and infinit points get a z=0.

The polar line to an infinite point (x0; y0; 0) is 2019.x0.x + 2020.y0.y = 0. The lines AC and BD are parallel and thus have such a point (x0, y0, 0) in common.

P is on the polar line and thus y0/x0 = -(20 * 2019)/(30 * 2020) = -673/1010 = - p/q.

p+q = 1683.

Ellipse Butterfly! - Part 1

The answer is 1683.

1 solution

0 pending reports