Ellipse Butterfly! - Part 2

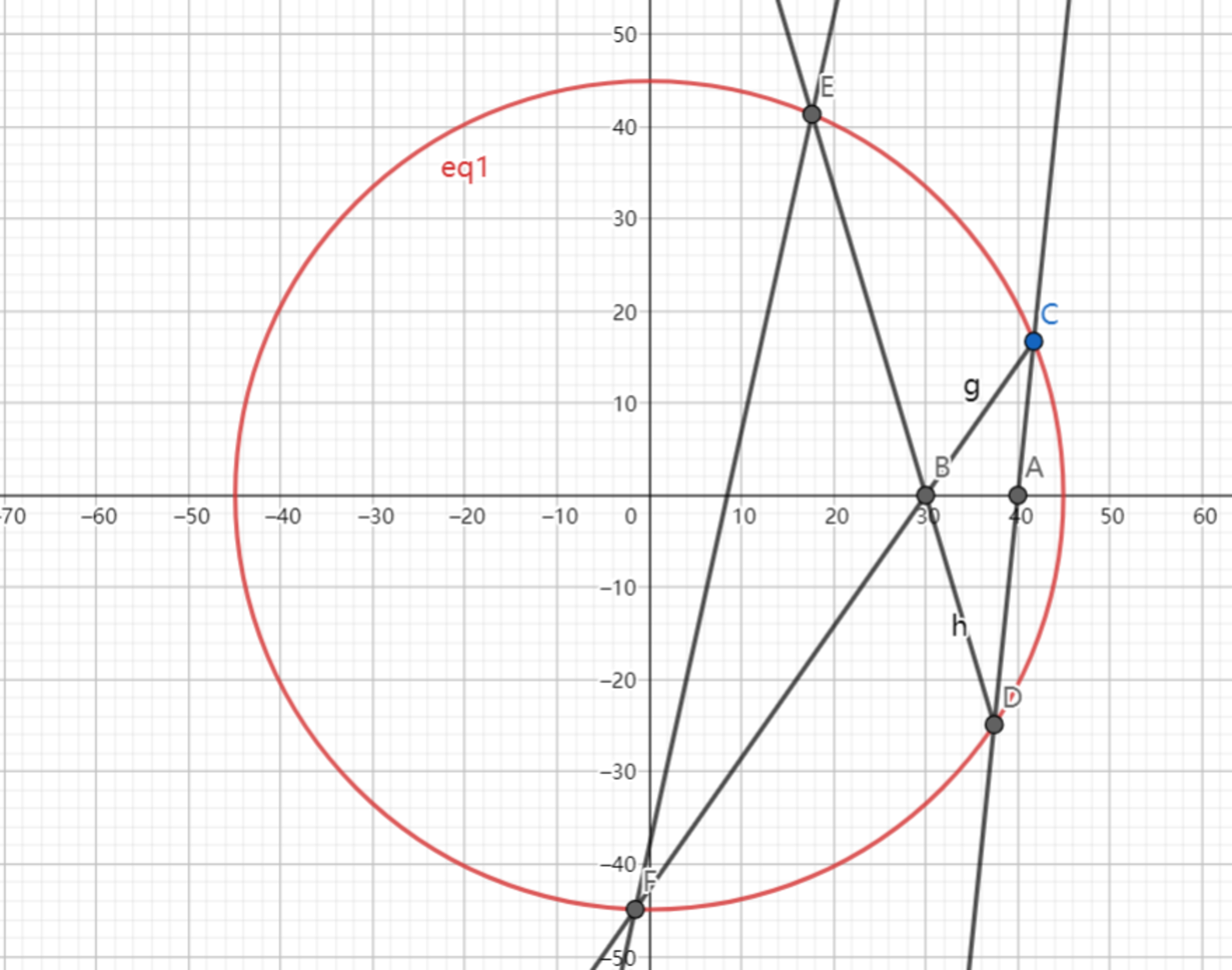
As shown above, the ellipse has equation: $\dfrac{x^2}{2020}+\dfrac{y^2}{2019}=1$ , $A(40,0)$ , $B(30,0)$ . Line $l_1$ passing through point $A$ intersects with the ellipse at point $C,D$ , line $BD, BC$ intersects with the ellipse at another point $E,F$ respectively, and line $l_2$ passes through $E$ and $F$ . $l_1$ has slope $k_1$ and $l_2$ has slope $k_2$ .

Then $\dfrac{k_2}{k_1}$ is always constant as $l_1$ rotates.

If the ratio can be expressed as $\dfrac{p}{q}$ , where $p,q$ are positive coprime integers. Submit $p+q$ .