Ellipse in an Open Rectangle
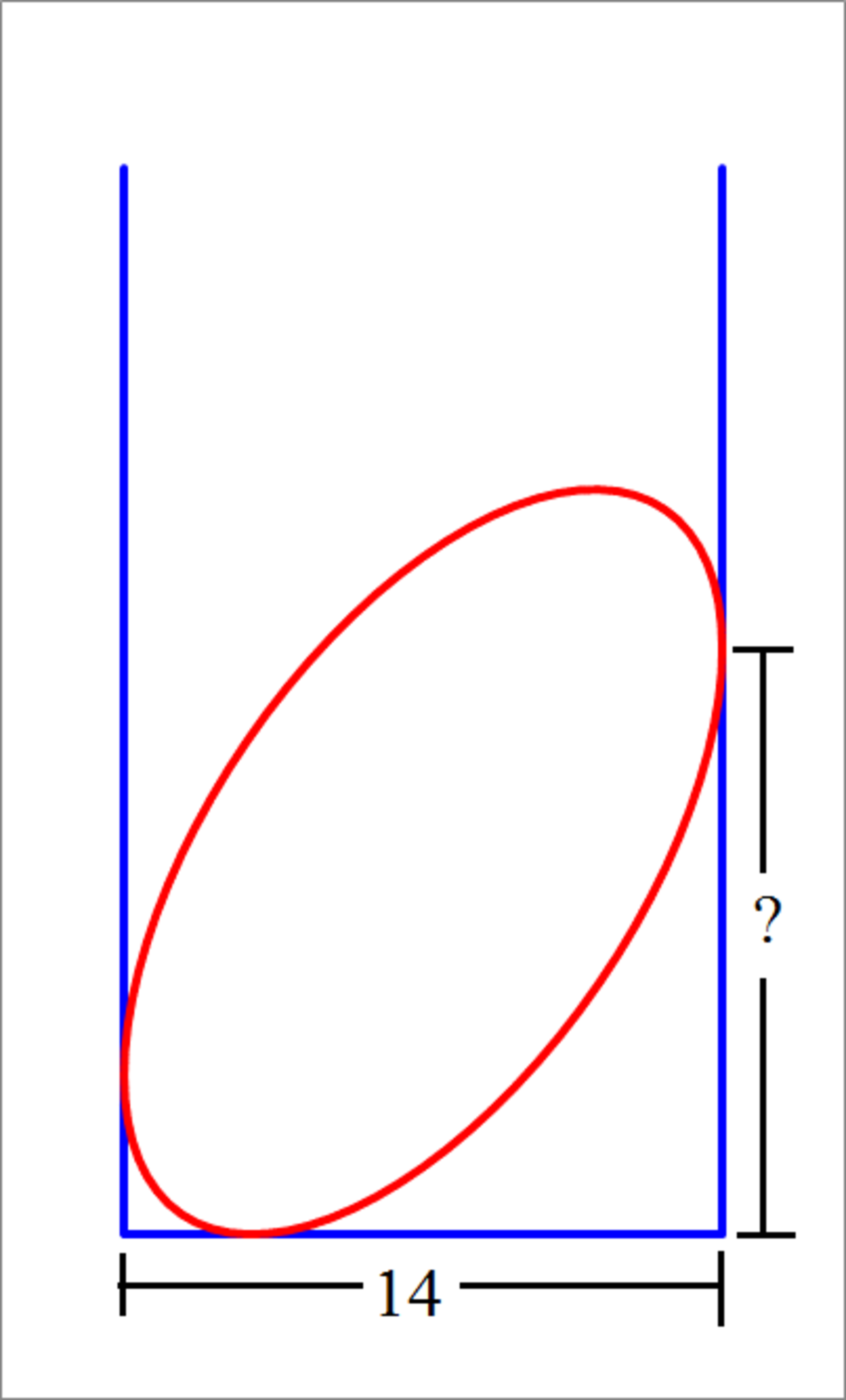
An ellipse rests in an open rectangle as shown in the figure above. The semi-axes of the ellipse of length 10, and 5, and the base of the rectangle is of length 14. The ellipse is tangent to both sides of the rectangle, as well as its base. How high above the base is the right tangency point?
The answer is 13.716.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The general equation for a rotated ellipse with semi-major axis a and semi-minor axis b and center r c = [ x c , y c ] T is
( r − r c ) T R D R T ( r − r c ) = 1
where r = [ x , y ] T , and
R = [ cos θ sin θ − sin θ cos θ ]
and
D = ⎣ ⎢ ⎡ a 2 1 0 0 b 2 1 ⎦ ⎥ ⎤
The gradient (the normal vector to the ellipse) at any point r on it is given by
g = 2 R D R T ( r − r c )
Now back to the problem. Let take the origin of the reference frame to be at the bottom left corner of the rectangle. From symmetry of the ellipse, it follows that
x c = 7
Now at the right tangency point r 1 , we have the gradient along the positive x-direction, so we can write
g / 2 = β [ 1 , 0 ] T
Using the gradient formula,
R D R T ( r 1 − r c ) = β [ 1 , 0 ] T
From which,
( r 1 − r c ) = β R D − 1 R T [ 1 , 0 ] T
Substituting this expression into the ellipse equation, results in,
β 2 [ 1 , 0 ] R D − 1 R T [ 1 , 0 ] T = 1
We now note that
R D − 1 R T = [ cos θ sin θ − sin θ cos θ ] [ a 2 0 0 b 2 ] [ cos θ − sin θ sin θ cos θ ]
Which simplifies to,
R D − 1 R T = [ a 2 cos 2 θ + b 2 sin 2 θ ( a 2 − b 2 ) sin θ cos θ ( a 2 − b 2 ) sin θ cos θ a 2 sin 2 θ + b 2 cos 2 θ ]
Therefore,
[ 1 , 0 ] R D − 1 R T [ 1 , 0 ] T = a 2 cos 2 θ + b 2 sin 2 θ
and hence,
β = a 2 cos 2 θ + b 2 sin 2 θ 1
Now the x-coordinate of ( r 1 − r c ) is
[ 1 , 0 ] ( r − r c ) = β [ 1 , 0 ] R D − 1 R T [ 1 , 0 ] T = a 2 cos 2 θ + b 2 sin 2 θ
But the x-coordinate of r 1 − r c is equal to 7 . Hence
a 2 cos 2 θ + b 2 sin 2 θ = 7 2 = 4 9
Substituting a = 1 0 and b = 5 , we can solve for θ ,
1 0 0 cos 2 θ + 2 5 sin 2 θ = 4 9
From which
θ = cos − 1 0 . 3 2 = 5 5 . 5 5 ∘
Let's find y c by applying the tangency condition on the tangency point with the bottom r 2 ,
Similar analysis to the above, leads to
[ 0 , 1 ] ( r 2 − r c ) = − γ [ 0 , 1 ] R D − 1 R T [ 0 , 1 ] T = − a 2 sin 2 θ + b 2 cos 2 θ
This implies that,
y c = a 2 sin 2 θ + b 2 cos 2 θ
Substituting the value of θ we just obtained, we have,
y c = 7 6 = 8 . 7 1 8
Finally, the y-coordinate of ( r 1 − r c ) is given by
[ 0 , 1 ] ( r 1 − r c ) = β [ 0 , 1 ] R D − 1 R T [ 1 , 0 ] T = 7 ( a 2 − b 2 ) sin θ cos θ
Substituting a , b , and θ , results in,
y 1 − y c = 4 . 9 9 8
Therefore,
y 1 = 4 . 9 9 8 + y c = 4 . 9 9 8 + 8 . 7 1 8 = 1 3 . 7 1 6