Ellipse Inscribed In A Square
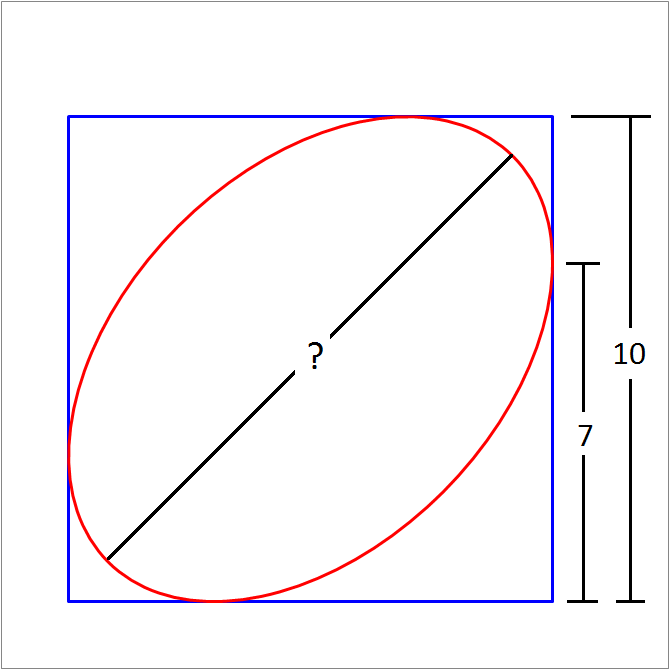
An ellipse is inscribed in a square of side length 10, as shown in the figure above. If the point of tangency on the right side is 7 units away from the bottom of the square, then find the length of the major axis of the ellipse.
Give your answer to 3 decimal places.
The answer is 11.832.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
 L
e
t
(
a
x
)
2
+
(
b
y
)
2
=
1
be the ellipse. AB the side of the square in first quadrant tangent to it. C the point of tangentcy.
I
t
c
a
n
b
e
s
e
e
n
f
r
o
m
s
y
m
m
e
t
r
y
t
h
a
t
A
(
0
,
5
2
)
,
B
(
5
2
,
0
)
,
m
=
s
l
o
p
e
A
B
=
−
1
.
F
r
o
m
t
h
e
F
i
g
.
C
(
2
7
,
2
3
)
But differentiating equation for ellipse we get
m
=
−
b
2
a
2
∗
x
y
.
B
u
t
m
=
−
1
.
⟹
m
c
=
−
b
2
a
2
∗
2
7
2
3
=
−
1
.
S
o
b
2
=
7
3
∗
a
2
.
.
.
.
.
.
.
(
∗
)
S
u
b
s
t
i
t
u
t
i
n
g
t
h
e
v
a
l
u
e
o
f
C
a
n
d
(
∗
)
i
n
t
h
e
e
q
u
a
t
i
o
n
o
f
t
h
e
e
l
l
i
p
s
e
,
w
e
g
e
t
,
a
=
3
5
.
S
o
m
a
j
o
r
−
a
x
i
s
=
2
a
=
1
1
.
8
3
2
.
L
e
t
(
a
x
)
2
+
(
b
y
)
2
=
1
be the ellipse. AB the side of the square in first quadrant tangent to it. C the point of tangentcy.
I
t
c
a
n
b
e
s
e
e
n
f
r
o
m
s
y
m
m
e
t
r
y
t
h
a
t
A
(
0
,
5
2
)
,
B
(
5
2
,
0
)
,
m
=
s
l
o
p
e
A
B
=
−
1
.
F
r
o
m
t
h
e
F
i
g
.
C
(
2
7
,
2
3
)
But differentiating equation for ellipse we get
m
=
−
b
2
a
2
∗
x
y
.
B
u
t
m
=
−
1
.
⟹
m
c
=
−
b
2
a
2
∗
2
7
2
3
=
−
1
.
S
o
b
2
=
7
3
∗
a
2
.
.
.
.
.
.
.
(
∗
)
S
u
b
s
t
i
t
u
t
i
n
g
t
h
e
v
a
l
u
e
o
f
C
a
n
d
(
∗
)
i
n
t
h
e
e
q
u
a
t
i
o
n
o
f
t
h
e
e
l
l
i
p
s
e
,
w
e
g
e
t
,
a
=
3
5
.
S
o
m
a
j
o
r
−
a
x
i
s
=
2
a
=
1
1
.
8
3
2
.
Nice solution! Just a minor typo in x coordinate of B line #2.
I used 'scaling of a circle' along y-axis. Found the height (y-coordinate of the point of tangency) on the circle as x y and then used Pythagoras to find the radius of the circle as 3 5
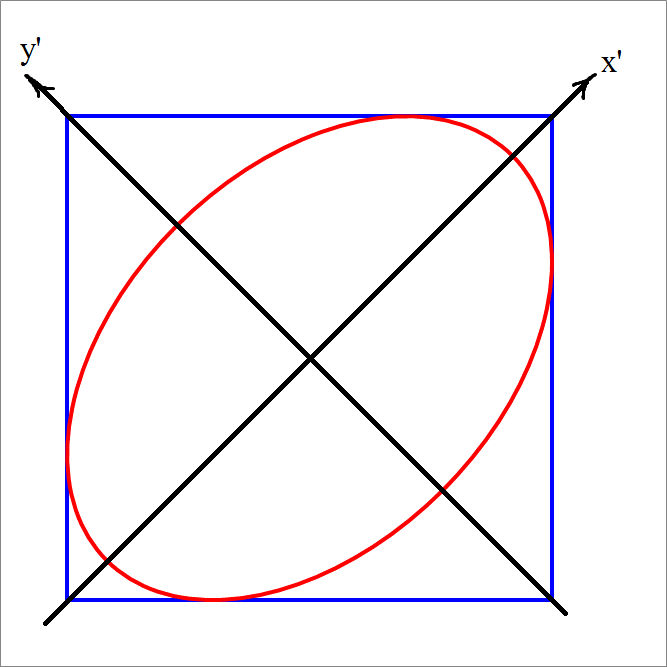
We'll define a rotated frame of reference X ′ Y ′ such that the ellipse major and minor axes are parallel to its axes, and the center of the ellipse, is at its origin. The angle of rotation is obviously 4 5 ∘ counterclockwise. We assume that the origin of original frame is at the left bottom corner of the square. This means that the center of the ellipse is the point ( 5 , 5 ) . Now it is straightforward to write the relation between ( x , y ) and ( x ′ , y ′ )
x ′ = 2 1 ( ( x − 5 ) + ( y − 5 ) ) = 2 1 ( ( x + y − 1 0 )
y ′ = 2 1 ( − ( x − 5 ) + ( y − 5 ) ) = 2 1 ( y − x )
The equation of the ellipse is
a 2 x ′ 2 + b 2 y ′ 2 = 1
The tangency point is (10, 7) in the original frame, so in terms of the new frame it becomes ( 2 7 , 2 − 3 ) .
The slope at the tangency point is 1 . Therefore, using the well-known formula for the slope of the ellipse at a point (x', y'):
d x ′ d y ′ = 1 = − ( a b ) 2 y ′ x ′ = 3 7 ( a b ) 2
so that
b 2 = 7 3 a 2 ⋯ ( 1 )
Now, substituting the given point in the equation of the ellipse,
2 a 2 4 9 + 2 b 2 9 = 1 ⋯ ( 2 )
Substituting (1) in (2),
2 a 2 4 9 + 6 a 2 6 3 = 1
From which,
6 a 2 2 1 0 = 1
hence,
a 2 = 6 2 1 0 = 3 5
Thus the semi-major axis is,
a = 3 5
Therefore, the major axis = 2 a = 2 3 5 = 1 1 . 8 3 2
See following graphic of a circle with a line that is tangent to it at 1 0 3 of the distance from the origin to where the line intersects the x -axis. The line intersects the y -axis at 1
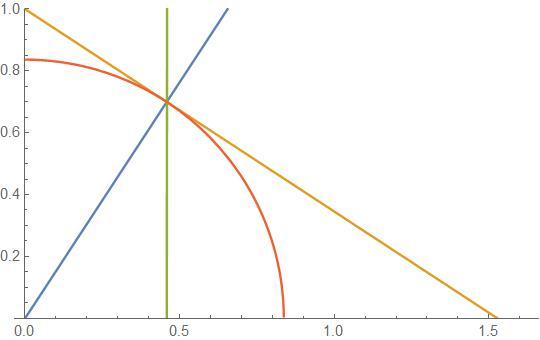
The radius of this circle can readily be found to be
1 0 7
We then first squeeze the figure along the x -axis so that the circle becomes an ellipse and the line has a slope of − 1 . We scale up the figure by a factor of
2 1 0
so that we have our square of sides 1 0 . For the length of the ellipse along its major axis, we compute
2 2 1 0 1 0 7 = 2 3 5 = 1 1 . 8 3 2 2 . . .
 Ellipse in Square
Ellipse in Square
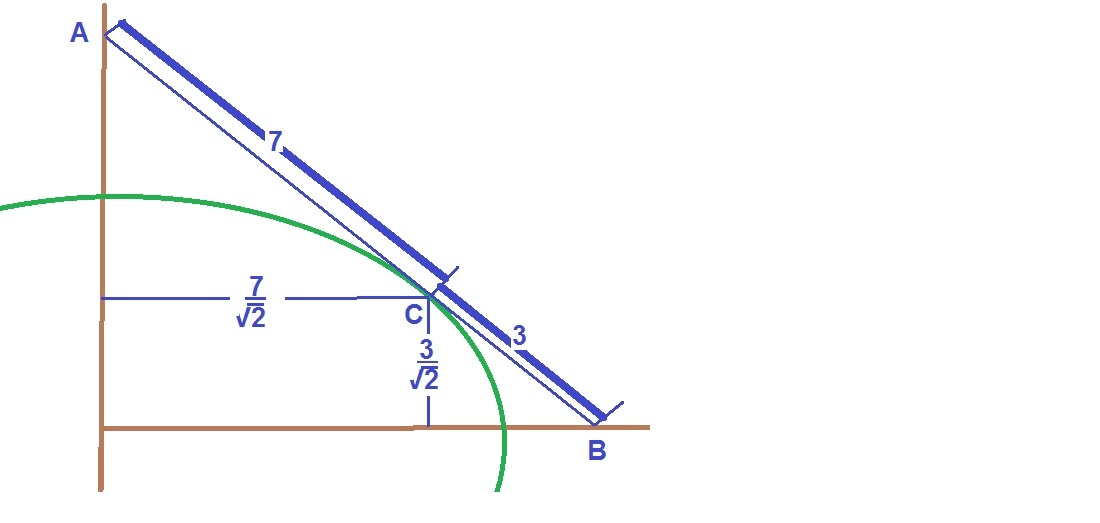
Taking the major axis as X axis and minor axis along Y. T = point of tangency, M = foot of the perpendicular from T on x axis. Slope of tangent AB = -1. BT = 7, TA = 3 given.
This gives coordinates: T ( 7 cos 4 5 ° , 3 sin 4 5 ° ) , A ( 1 0 cos 4 5 ° , 0 ) giving distances O M = 2 7 M A = 2 3
Project point of tangency T up to point of tangency T' on the parent circle. OT'A = 90° giving MT' ^2 = OM \times MA and the radius = semi major axis O M 2 + M T ′ 2 = 3 5 and the major axis 2 3 5 = 11.832
We know director radius √(a^2+b^2) = 1/2 diagonal of square(10/√2). And selecting axes along diagonal of square we get coordinate of a pt lining on ellipse to be 7/√2 and 3/√2 hence putting these pt in standard ellipse form we get another eq in a^2,b^2 solving both to get 11.832