Ellipse Inscribed in a Trapezoid
Calculus
Level
4
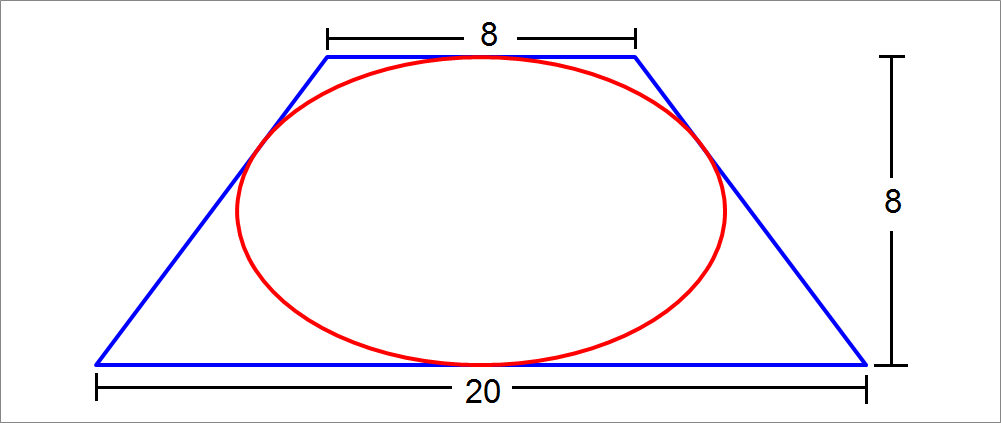
An isosceles trapezoid has the two parallel bases of lengths 20 and 8, and an altitude of 8. An ellipse is drawn to fit within it. Find the length of its major axis.
The answer is 12.649.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Utilizing symmetry, we can consider only one half of the given figure,
We apply horizontal scaling to bring half the ellipse into a semi-circle.
The scaled upper base will have a length of ( 4 s ) , and the lower base will have a length of ( 1 0 s ) . where s is the scale factor.
Using the result of this problem , we have the following relation,
( 4 s ) ( 1 0 s ) = ( radius of semi-circle ) 2 = 4 2 = 1 6
Hence s = 5 2
Hence ellipse semi-major axis = a = s 4 = 4 2 5 = 4 0
From which, the major axis = 2 a = 2 4 0 = 1 2 . 6 4 9 .