Ellipse intersections
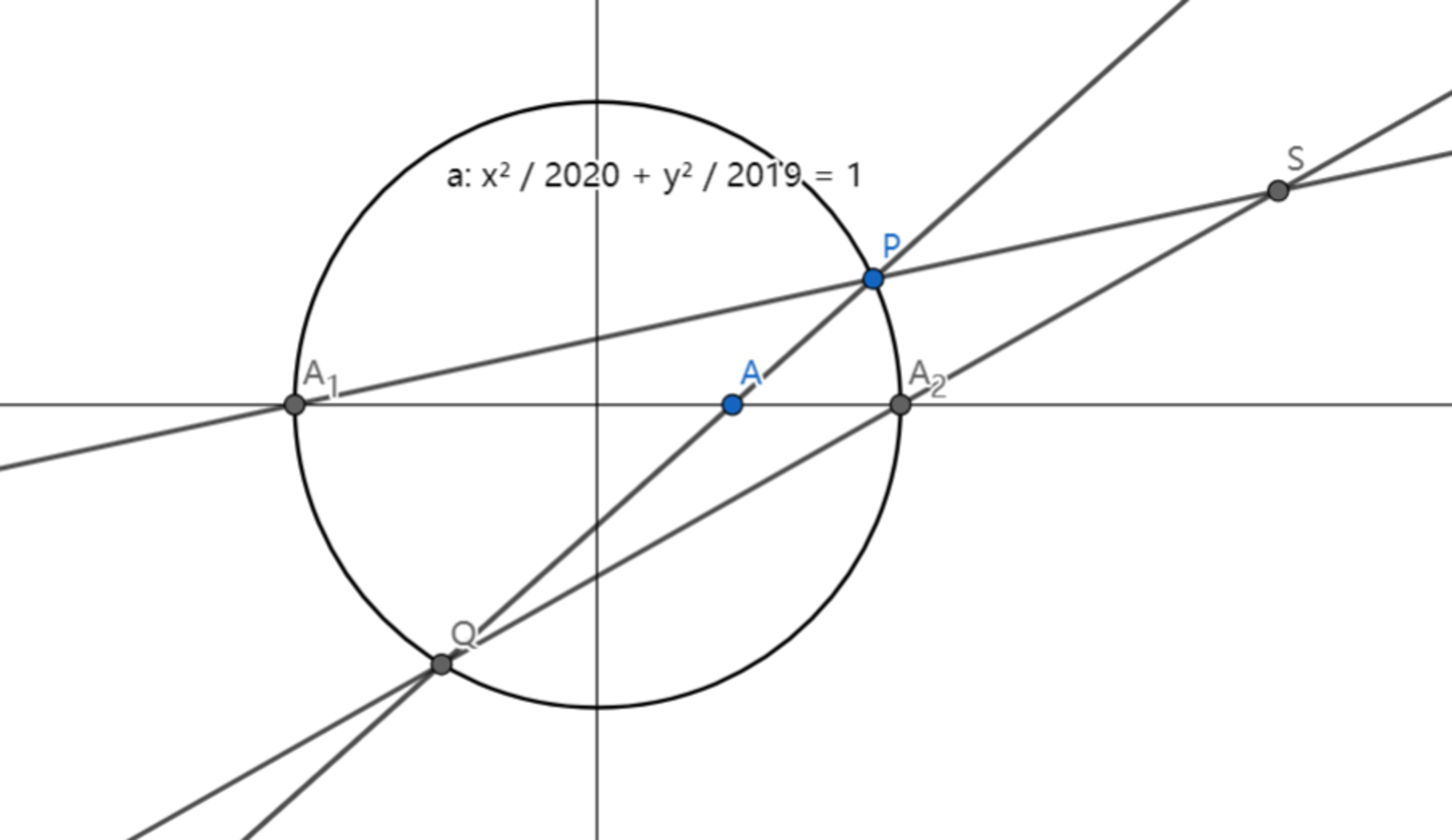
The ellipse: 2 0 2 0 x 2 + 2 0 1 9 y 2 = 1 intersects with x -axis at A 1 and A 2 , A is a point between A 1 A 2 and P is an arbitrary point on the ellipse. A P intersects with the ellipse at another point Q .
As the picture shows, lines A 1 P and A 2 Q intersect at point S , then as P moves, S is always on the line: x = λ .
Given that A has the coordinate ( 2 0 , 0 ) , find the value of λ .
The answer is 101.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
If the equation of the ellipse be a 2 x 2 + b 2 y 2 = 1 and the position coordinates of A be ( p , 0 ) , then the locus of S is x = p a 2 . In this question, a 2 = 2 0 2 0 , p = 2 0 . So the locus of S is x = 2 0 2 0 2 0 = 1 0 1 . So λ = 1 0 1 .
Choose P with coordinates ( 2 0 , q ) . Then P A is a vertical line, and by symmetry Q has coordinates ( 2 0 , − q ) . From the equation of the ellipse, A 1 has coordinates ( − 2 0 2 0 , 0 ) and A 2 has coordinates ( 2 0 2 0 , 0 ) .
The equation of the line A 1 P is then y = 2 0 2 0 + 2 0 q ( x + 2 0 2 0 ) and the equation of the line Q A 2 is y = 2 0 2 0 − 2 0 q ( x − 2 0 2 0 ) .
Since S is on both A 1 P and Q A 2 , 2 0 2 0 + 2 0 q ( λ + 2 0 2 0 ) = 2 0 2 0 − 2 0 q ( λ − 2 0 2 0 ) , which solves to λ = 1 0 1 .