Ellipse "inversion"
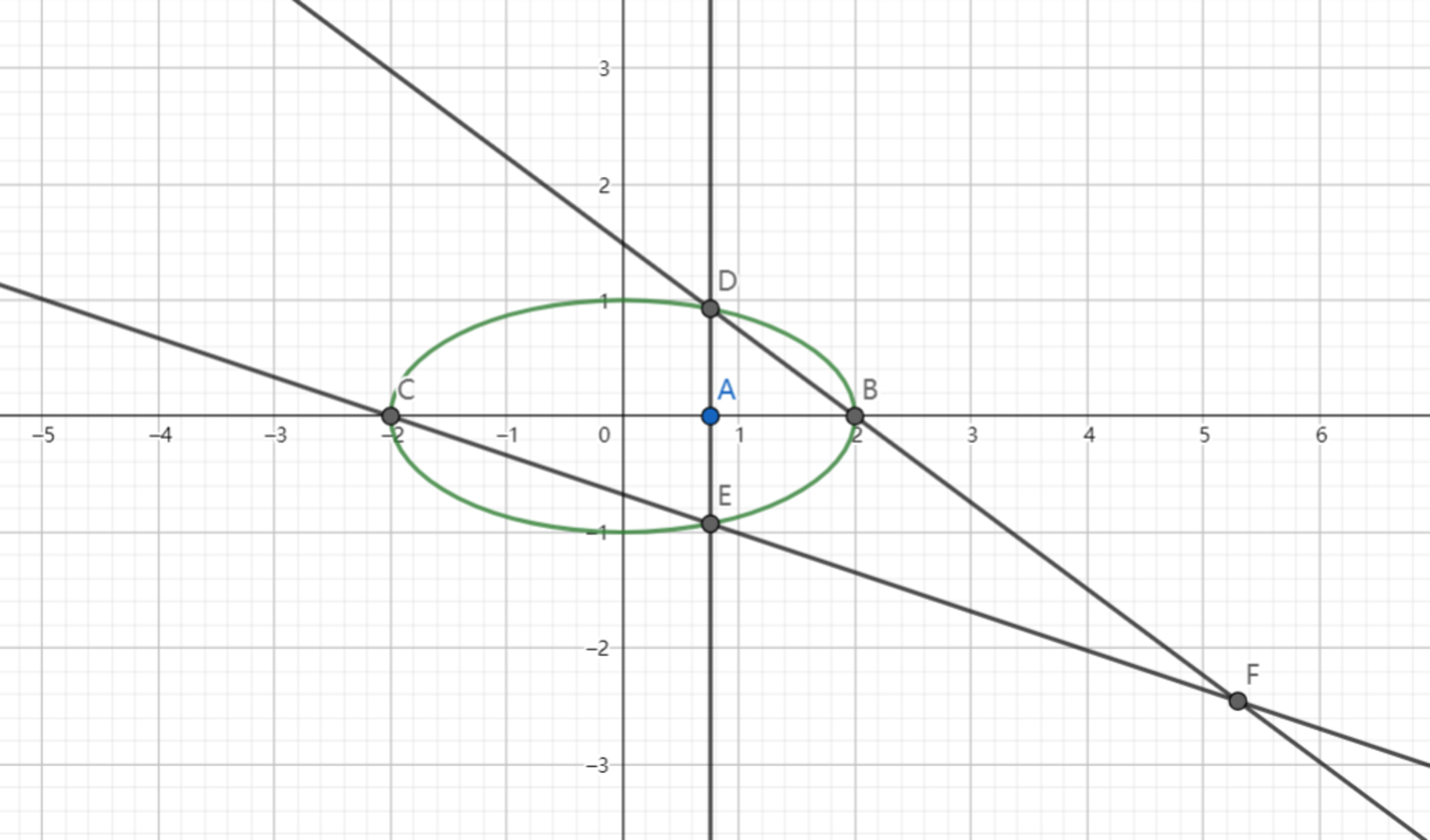
The ellipse show above has equation: a 2 x 2 + b 2 y 2 = 1 , where (a>b>0)). Points B and C are the right and left vertices of the ellipse respectively. Point A is a moving point along the x -axis between B and C . The line through A perpendicular to B C intersects the ellipse at points D and E ( D and E can be on either side). If we extend B D and C E , they meet at point F , what is the locus of point F as A moves?
Bonus: Find the equation of the locus.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Since B , C , D and E are on the ellipse, we can assign their coordinates as B ( a , 0 ) , C ( − a , 0 ) , D ( a cos θ , b sin θ ) and E ( a cos θ , − b sin θ ) . Then the equations for lines D F and C F are:
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ D F : C F : x − a y − 0 = a cos θ − a b sin θ − 0 x + a y − 0 = a cos θ + a − b sin θ − 0 ⟹ y = a ( cos θ − 1 ) b sin θ ( x − a ) ⟹ y = a ( cos θ + 1 ) b sin θ ( x + a )
Then the coordinates of F are given by:
a ( cos θ − 1 ) b sin θ ( x F − a ) ( a − x F ) ( cos θ + 1 ) ⟹ x F D F : y F = a ( cos θ + 1 ) − b sin θ ( x F + a ) = ( a + x F ) ( cos θ − 1 ) = cos θ a = a sec θ = a ( cos θ − 1 ) b sin θ ( a sec θ − a ) = cos θ ( cos θ − 1 ) b sin θ ( 1 − cos θ ) = − b tan θ
Then a 2 x F 2 − b 2 y F 2 = sec 2 θ − tan 2 θ = 1 , which is a hyperbola .
The locus of the point F is a 2 x 2 − b 2 y 2 = 1 .
Proof :- Let at any position of A , it's coordinates be ( h , 0 ) . Then those of D are ( h , a b a 2 − h 2 ) and of E are ( h , − a b a 2 − h 2 ) . Therefore the equation of D B is y = − a b a − h a + h ( x − a ) , and of C E is y = − a b a + h a − h ( x + a ) . Hence the coordinates of F are ( h a 2 , − h b a 2 − h 2 ) . Therefore the locus of F is y 2 = a 2 b 2 x 2 − b 2 or a 2 x 2 − b 2 y 2 = 1