Ellipse Mania!
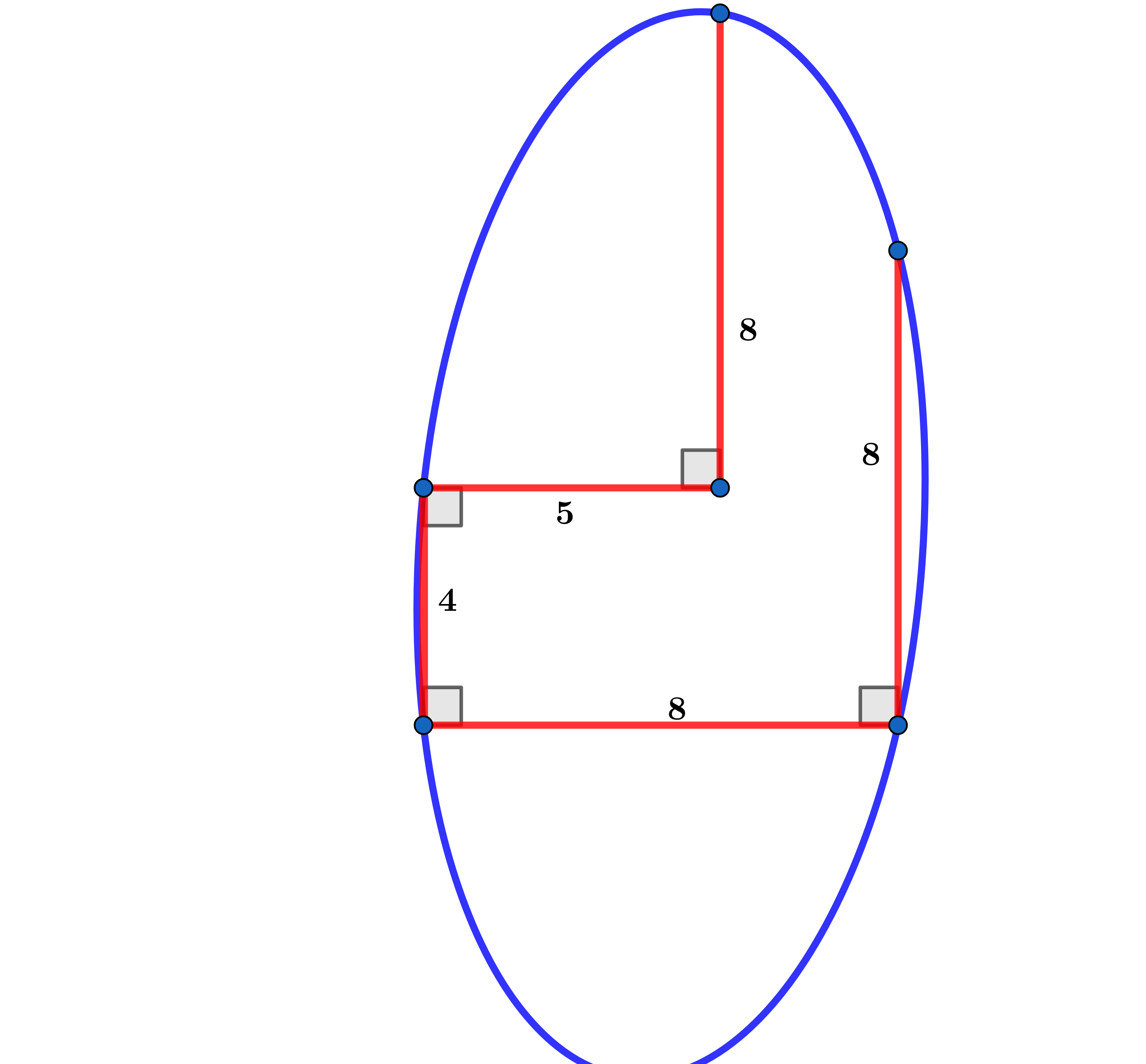
If the area A of the ellipse above can be represented as A = β 2 3 λ α π , where α , β and λ are coprime positive integers, find α + β + λ .
The answer is 552288.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
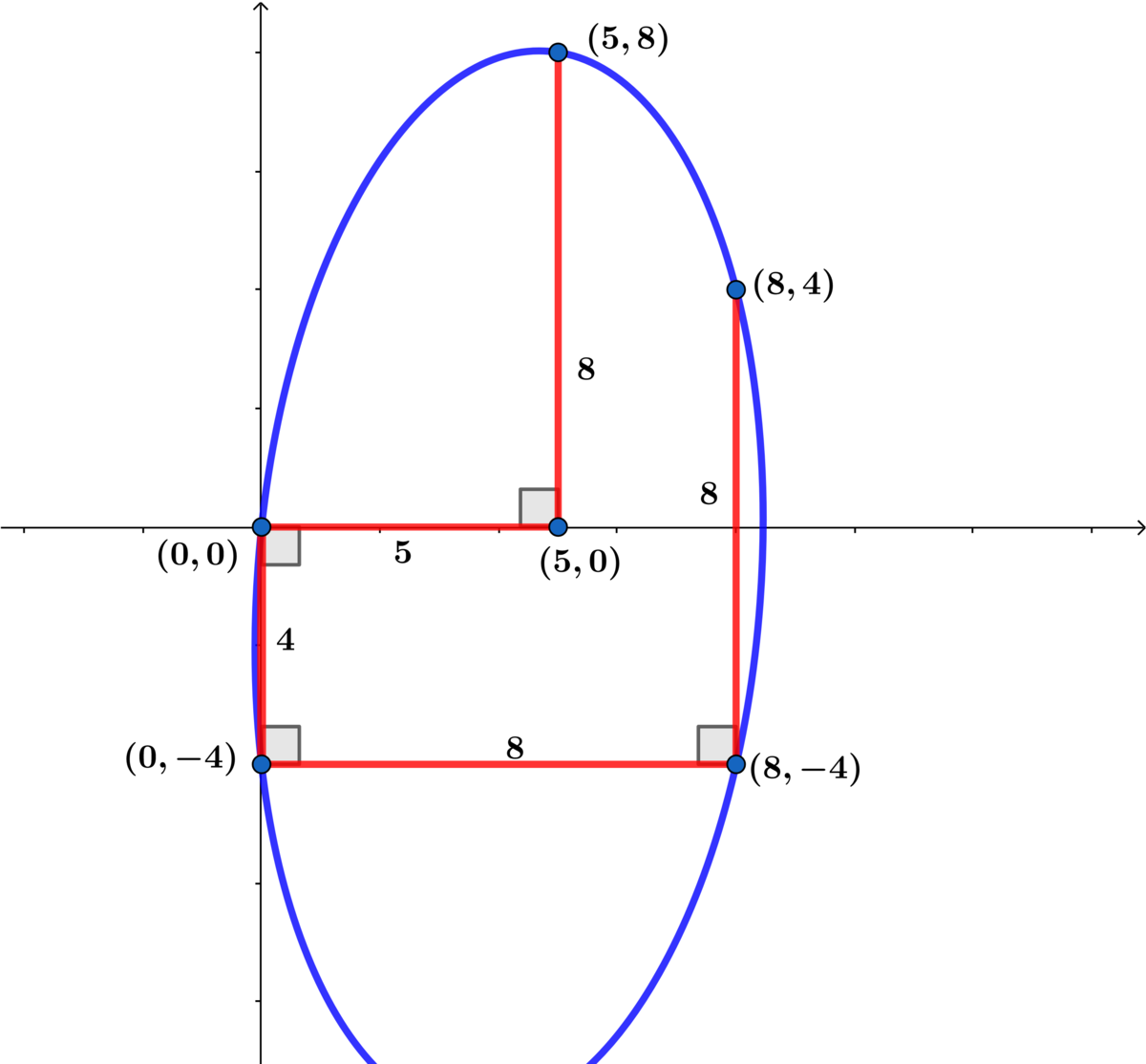
Using a x 2 + b x y + c y 2 + d x + e y = 0 and the points I chose above to generate the ellipse.
(1) ( 0 , − 4 ) : 4 c − e = 0 ⟹ c = 4 e
(2) ( 8 , 4 ) : 1 6 a + 8 b + 4 c + 2 d + e = 0
(3) ( 8 , − 4 ) : 1 6 a − 8 b + 4 c + 2 d − e = 0
Subtracting (3) from (2) we obtain: 8 b + e = 0 ⟹ b = − 8 e
(4) ( 5 , 8 ) : 2 5 a + 4 0 b + 6 4 c + 5 d + 8 c = 0
Replacing c = 4 e and b = − 8 e into (2) and (4) ⟹
1 6 a + 2 d = − e
2 5 a + 5 d = − 1 9 e
⟹ a = 1 0 1 1 e and d = − 1 0 9 3 e
⟹ 1 0 1 1 x 2 − 8 1 x y + 4 1 y 2 − 1 0 9 3 x + y = 0 ⟹ 4 4 x 2 − 5 x y + 1 0 y 2 − 3 7 2 x + 4 0 y = 0 ⟹ 1 0 y 2 + 5 ( x − 8 ) y + 4 4 x 2 − 3 7 2 x = 0
Solving for y we obtain:
y = 4 x − 8 ± 2 0 1 3 4 7 5 2 2 0 7 7 4 4 − ( 3 4 7 x − 1 4 4 8 ) 2 .
y ( x ) = 4 x − 8 + 2 0 1 3 4 7 5 2 2 0 7 7 4 4 − ( 3 4 7 x − 1 4 4 8 ) 2 for the portion of the ellipse above the line y = 4 x − 8 .
Setting 2 2 0 7 7 4 4 − ( 3 4 7 x − 1 4 4 8 ) 2 = 0 ⟹ x = 3 4 7 1 4 4 8 ± 4 4 8 1 1 are the points of intersection of the ellipse and the line 4 x − 8 .
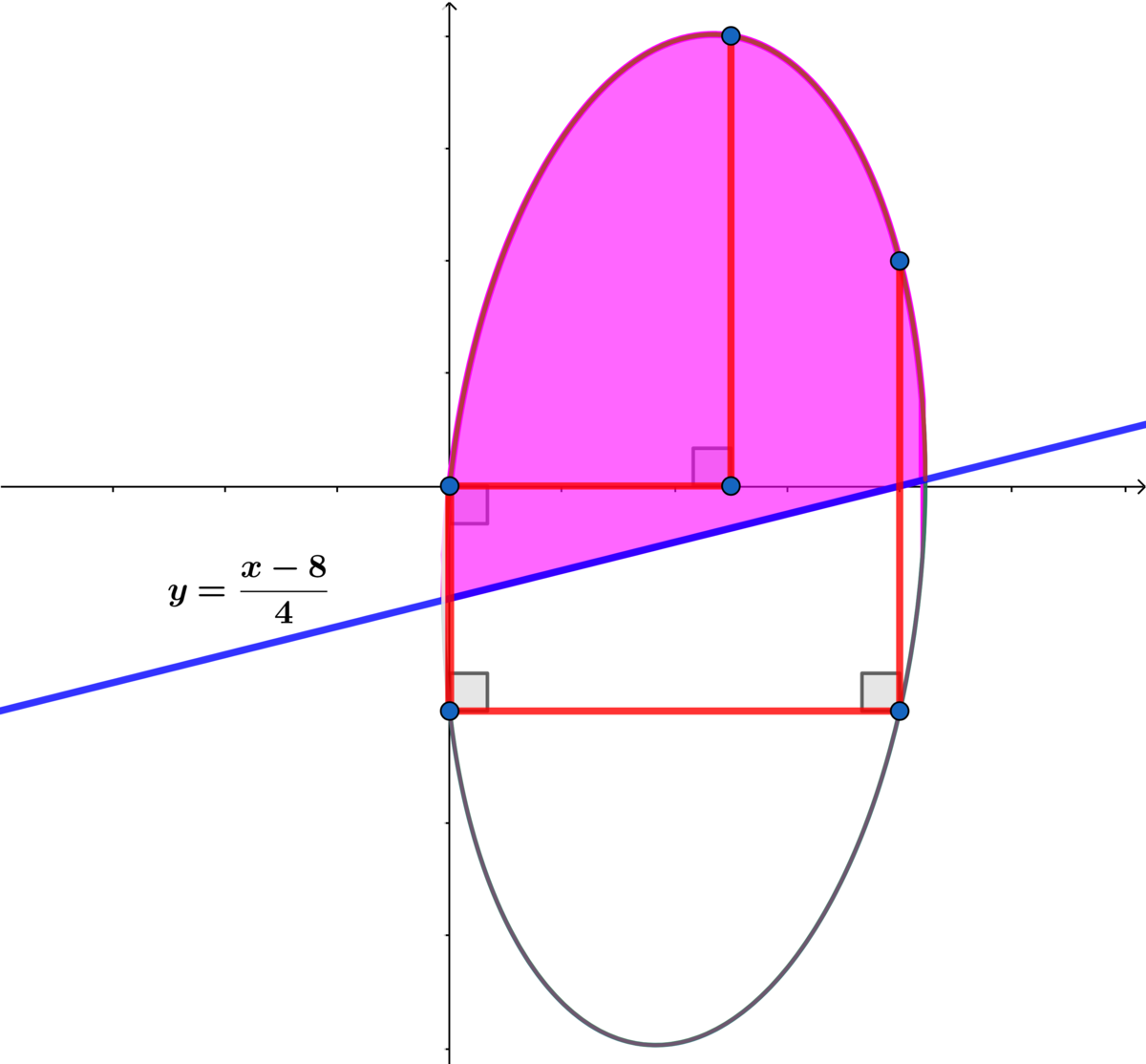
Letting
a
=
3
4
7
1
4
4
8
−
4
4
8
1
1
and
b
=
3
4
7
1
4
4
8
+
4
4
8
1
1
the area of the ellipse is
A
=
2
∫
a
b
y
(
x
)
−
4
x
−
8
d
x
=
1
0
1
3
4
7
5
∫
a
b
2
2
0
7
7
4
4
−
(
3
4
7
x
−
1
4
4
8
)
2
d
x
=
2
5
3
4
7
1
∫
a
b
2
2
0
7
7
4
4
−
(
3
4
7
x
−
1
4
4
8
)
2
d
x
.
For I ( x ) = ∫ 2 2 0 7 7 4 4 − ( 3 4 7 x − 1 4 4 8 ) 2 d x
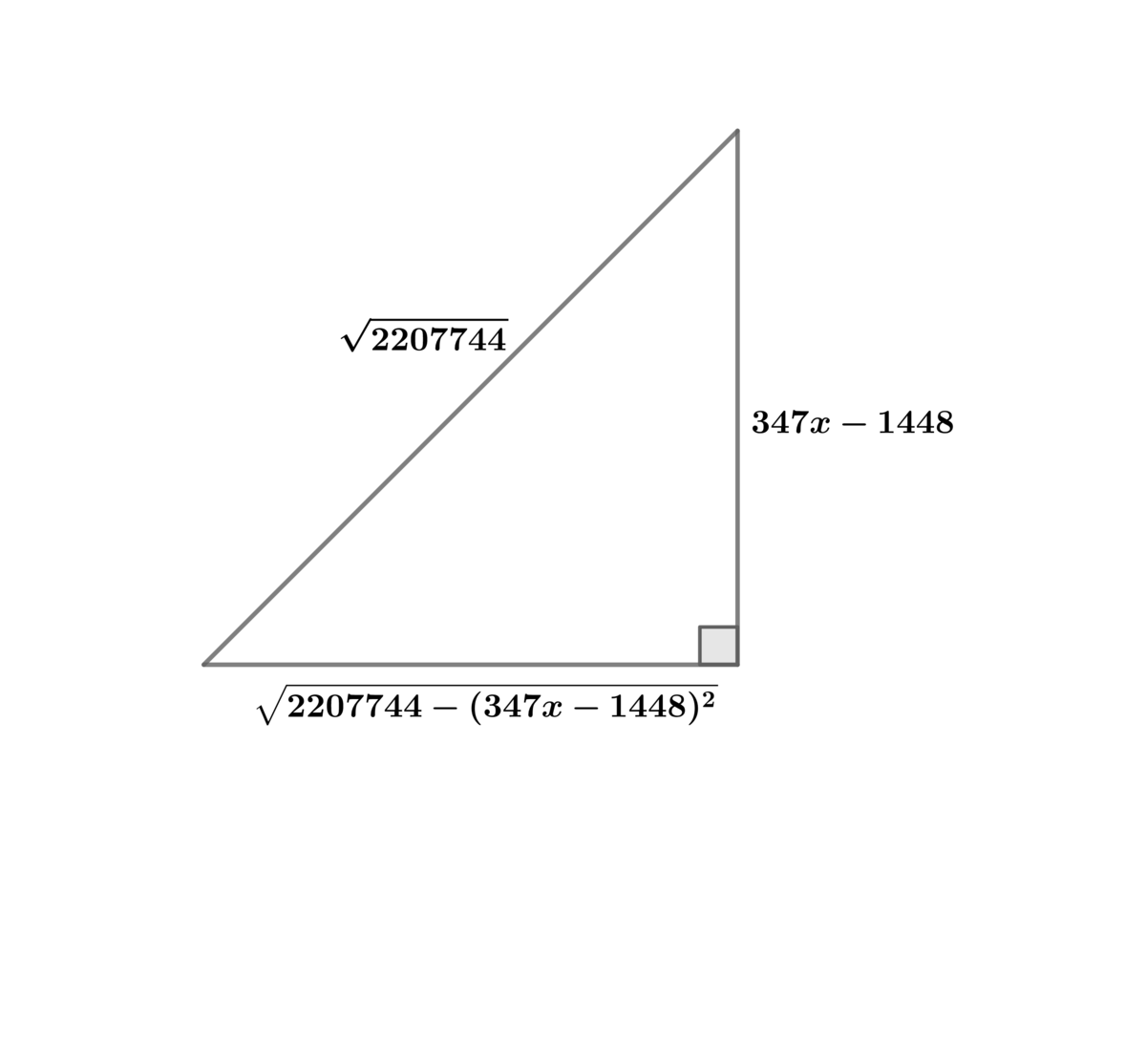
Let 3 4 7 x − 1 4 4 8 = 2 2 0 7 7 4 4 sin ( θ ) ⟹ d x = 3 4 7 2 2 0 7 7 4 4 cos ( θ )
⟹ I ( θ ) = 3 4 7 2 2 0 7 7 4 4 ∫ cos 2 ( θ ) d θ = 6 9 4 2 2 0 7 7 4 4 ∫ ( 1 + cos ( 2 θ ) ) d θ = 6 9 4 2 2 0 7 7 4 4 ( θ + sin ( θ ) cos ( θ ) )
⟹ I ( x ) = 6 9 4 2 2 0 7 7 4 4 ( arcsin ( 2 2 0 7 7 4 4 3 4 7 x − 1 4 4 8 ) + 2 2 0 7 7 4 4 3 4 7 x − 1 4 4 8 2 2 0 7 7 4 4 − ( 3 4 7 x − 1 4 4 8 ) 2 ) ⟹
A = ( 3 4 7 ) 2 3 5 5 5 1 9 3 6 ( arcsin ( 2 2 0 7 7 4 4 3 4 7 x − 1 4 4 8 ) + 2 2 0 7 7 4 4 3 4 7 x − 1 4 4 8 2 2 0 7 7 4 4 − ( 3 4 7 x − 1 4 4 8 ) 2 ) ∣ a b = ( 3 4 7 ) 2 3 5 1 1 0 3 8 7 2 ( 2 π ) =
( 3 4 7 ) 2 3 5 5 5 1 9 3 6 π = β 2 3 λ α π ⟹ α + β + λ = 5 5 2 2 8 8 .
First we set a coordinate system as depicted in the figure: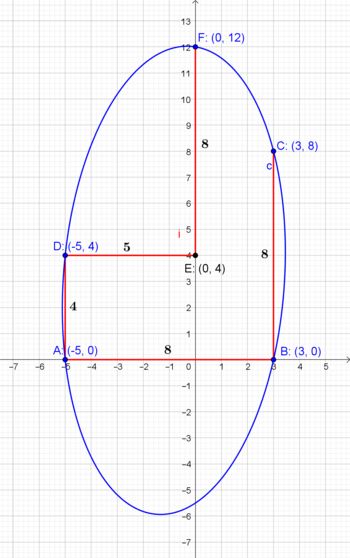 As we can see
here
the equation of the conic containing five points
(
x
i
,
y
i
)
i
=
1
,
2
,
3
,
4
,
5
, is
As we can see
here
the equation of the conic containing five points
(
x
i
,
y
i
)
i
=
1
,
2
,
3
,
4
,
5
, is
det ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 2 x 1 2 x 2 2 x 3 2 x 4 2 x 5 2 x y x 1 y 1 x 2 y 2 x 3 y 3 x 4 y 4 x 5 y 5 y 2 y 1 2 y 2 2 y 3 2 y 4 2 y 5 2 x x 1 x 2 x 3 x 4 x 5 y y 1 y 2 y 3 y 4 y 5 1 1 1 1 1 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = 0 In our case, using the points A , B , C , D and F , the equation of the ellipse is
det ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ x 2 2 5 9 1 6 0 9 x y 0 0 0 0 2 4 y 2 0 0 0 1 4 4 6 4 x − 5 3 − 4 0 3 y 0 0 0 1 2 8 1 1 1 1 1 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = 0 ⇔ 4 4 x 2 − 5 x y + 1 0 y 2 + 8 8 x − 6 5 y − 6 6 0 = 0 The later is of the form
a x 2 + 2 b x y + c y 2 + 2 d x + 2 f y + g = 0 with a = 4 4 b = 2 − 5 c = 1 0 d = 4 4 f = 2 − 6 5 g = − 6 6 0
The corresponding formulae for the semi-axes a ′ , b ′ of the ellipse are a ′ , b ′ = ± ( b 2 − a c ) [ ( a − c ) 2 + 4 b 2 − ( a + c ) ] 2 ( a f 2 + c d 2 + g b 2 − 2 b d f − a c g ) Taking their product and applying the numerical values we have a ′ b ′ = ( a c − b 2 ) 2 3 a f 2 + c d 2 + g b 2 − 2 b d f − a c g = ( 4 4 × 1 0 − ( − 2 5 ) 2 ) 2 3 4 4 × ( − 2 6 5 ) 2 + 1 0 × 4 4 2 + ( − 6 6 0 ) ( − 2 5 ) 2 − 2 × ( − 2 5 ) × 4 4 × ( − 2 6 5 ) − 4 4 × 1 0 × ( − 6 6 0 ) = 3 4 7 1 7 3 5 5 5 1 9 3 6 = 3 4 7 3 4 7 × 5 5 5 1 9 3 6 = 3 4 7 2 3 5 5 5 1 9 3 6 Consequently, the area of the ellipse is
A = a ′ b ′ π = 3 4 7 2 3 5 5 5 1 9 3 6 π For the answer, α = 5 5 1 9 3 6 , β = 3 4 7 , λ = 5 , thus, α + β + λ = 5 5 2 2 8 8 .