Ellipse Sector Area
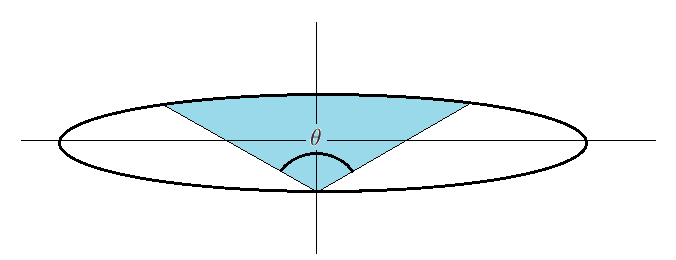
The above ellipse has a semi-major axis length of 5 and a semi-minor axis length of 1. If the blue sector accounts for half the area of the ellipse, what is the value of the angle , in degrees, to the nearest degree?
The answer is 131.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the intersection of the line originating at (0,-1) and the positive part of the ellipse in the first quadrant be (x 0,y 0). Let P be the intersection of the x axis be denoted by P, and for convenience, we shall also call the distance from the origin to point P as P. Let F = point(x 0,y 0), O = origin, D = (0,-1), and E = (0,1), and finally G = (x 0,0). Then the area EDF will be 1/4 of the area of the ellipse , which is 5*pi/4. The equation of the ellipse is x^2/25 + y^2/1 = 1.The area EDF = area of OEFG - area of triangle PFG + area of triangle OFD.These areas are respectfully given as integral from 0 to x 0 of y(dx) - (1/2)(y 0)(X 0 - p) + (1/2)p..solving for y, y =sqrt(25-x^2)/5.P can be found in terms of x 0,y 0 from x 0 -P =sqrt((y 0)^2 + (x 0 - P)^2) - (y 0)^2, which yields P = (x 0)/((y 0) + 1). Using standard integration techniques(substitution), we find the necessary equation which must be solved for x 0. It Is (5/2)*{arcsin(x 0)/5) + ((x 0)/25)*sqrt(25 - (x 0)^2))} + ((x 0)/2)*[1 -sqrt(25 - (x 0)^2)/5] = 5*pi/4. The equation is solved numerically, giving a root close to x 0 = 3.69. Then y 0 = .6748, and P =2.203. Finally tan(theta/2) = P/1, and Theta rounded is 131. Ed Gray