Ellipses and Circles
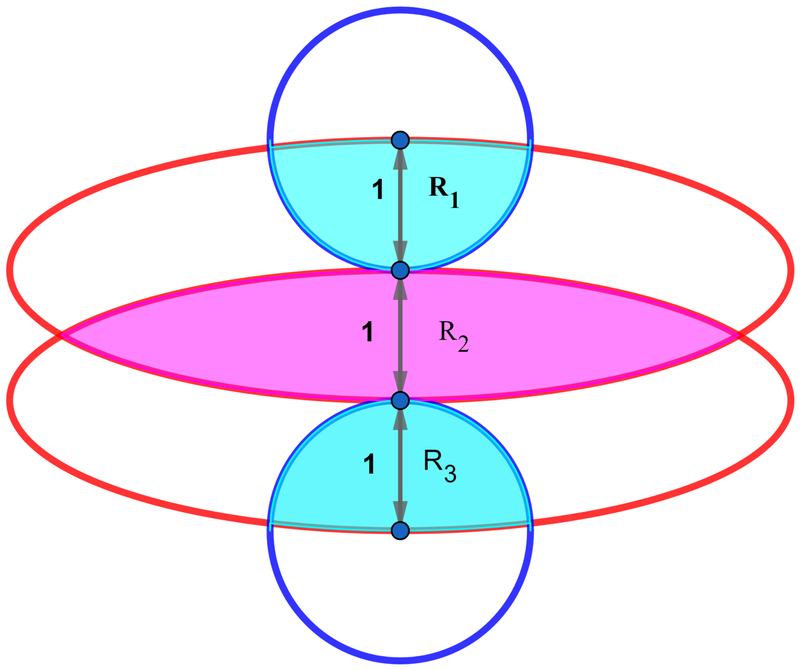
The length of the semi-major and semi-minor axis of the two congruent ellipses above are units and unit respectively and the two congruent circles have a radius of .
If the centers of the ellipses and circles are all unit apart as shown above, find the total area of the shaded regions above.
The answer is 6.7508165.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For Region 2 :
I chose the ellipses ( 9 x 2 + y 2 = 1 above the line y = 0 ) and ( 9 x 2 + ( y − 1 ) 2 = 1 below the line y = 1 ) .
Solving for y in both ellipses we want:
f ( x ) = 3 1 9 − x 2 and g ( x ) = 1 − 3 1 9 − x 2 .
f ( x ) = g ( x ) ⟹ x = ± 2 3 3 ⟹ the area A 2 = ∫ − 2 3 3 2 3 3 f ( x ) − g ( x ) d x = 3 2 ∫ − 2 3 3 2 3 3 9 − x 2 d x − 3 3
For I = 3 2 ∫ − 2 3 3 2 3 3 9 − x 2 d x
Let x = 3 sin ( θ ) ⟹ d x = 3 cos ( θ ) ⟹ I = 6 ∫ − 3 π 3 π cos 2 ( θ ) d θ = 3 ∫ − 3 π 3 π 1 + cos ( 2 θ ) d θ = 3 ( θ + 2 1 sin ( 2 θ ) ) ∣ − 3 π 3 π = 2 π + 2 3 3 ⟹ A 2 = 2 π − 2 3 3 ≈ 3 . 6 8 5 1 0 9 1
I chose the circles x 2 + ( y − 2 ) 2 = 1 and x 2 + ( y + 1 ) 2 = 1 .
Note by symmetry A 3 = A 1 .
For Region 1 :
Using the portion of the ellipse ( m ( x ) = 1 + 3 1 9 − x 2 above the line y = 1 ) and the circle ( h ( x ) = 2 − 1 − x 2 below the line y = 2 ) and setting h ( x ) = m ( x ) ⟹
9 − x 2 + 3 1 − x 2 = 3 ⟹ − 1 0 x 2 + 9 + 6 9 − 1 0 x 2 + x 4 = 0 ⟹ 3 2 4 − 3 6 0 x 2 + 3 6 x 4 = 1 0 0 x 4 − 1 8 0 x 2 + 8 1
⟹ 6 4 x 4 + 1 8 0 x 2 − 2 4 3 = 0 ⟹ x 2 = 3 2 9 ( − 5 ± 7 3 ) ⟹ x 1 , x 2 = ± 8 3 2 7 3 − 5 dropping the two imaginary roots.
A 1 = ∫ x 1 x 2 3 1 9 − x 2 + 1 − x 2 d x − 4 3 2 7 3 − 5 .
Let x = sin ( θ ) ⟹ d x = cos ( θ ) d θ ⟹ ∫ 1 − x 2 d x = 2 1 ( θ + sin ( θ ) cos ( θ ) ) = 2 1 ( arcsin ( x ) + x 1 − x 2 )
Let x = sin ( λ ) ⟹ d x = cos ( λ ) d λ ⟹ 3 1 ∫ 9 − x 2 d x = 2 3 ( λ + sin ( λ ) cos ( λ ) ) = 2 3 ( arcsin ( 3 x ) + 3 x 9 − x 2 )
⟹ I = ∫ x 1 x 2 3 1 9 − x 2 + 1 − x 2 d x = 2 1 ( arcsin ( x ) + 3 arcsin ( 3 x ) + x ( 1 − x 2 + 3 9 − x 2 ) ) ∣ x 1 x 2 =
arcsin ( x 2 ) + 3 arcsin ( 3 x 2 ) + x 2 ( 1 − x 2 2 + 3 9 − x 2 2 )
Using x 2 ≈ 0 . 9 9 8 3 7 4 2 ⟹ I = 3 . 5 2 9 6 0 2 1 ⟹ A 1 = 3 . 5 2 9 6 0 2 1 − 2 ∗ x 2 = 3 . 5 2 9 6 0 2 1 − 1 . 9 9 6 7 4 8 4 = 1 . 5 3 2 8 5 3 7
⟹ A T o t a l = A 2 + 2 A 1 = 3 . 6 8 5 1 0 9 1 + 2 ( 1 . 5 3 2 8 5 3 7 ) = 6 . 7 5 0 8 1 6 5 .
Note: I could not put any functions in the ellipse - circle diagram because the latex in Geogebra no longer works.