Ellipse's Circular Tangents
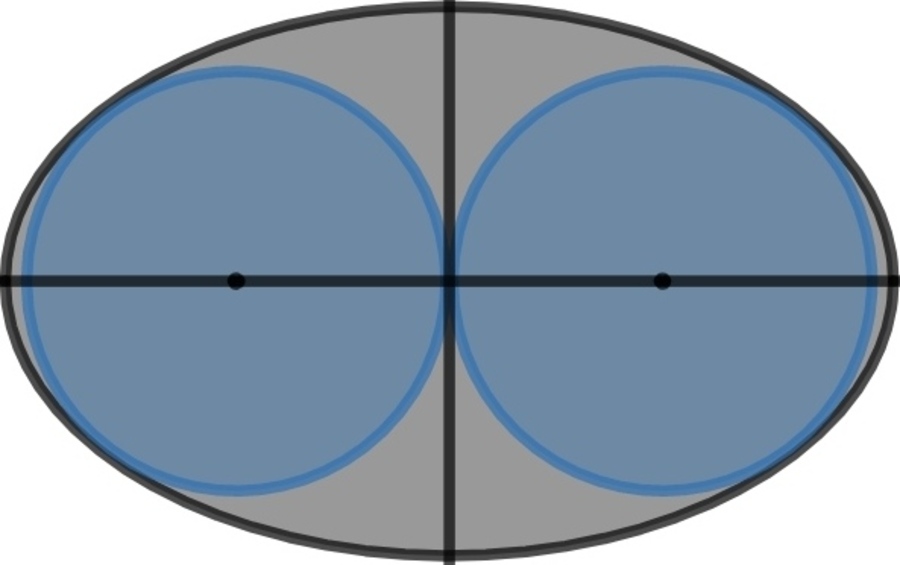
Inside an ellipse, two circles are drawn which touch the minor axis of the ellipse and also touch the ellipse at the ends of latus rectum. The combined area of the two circles is A 1 and area of ellipse is A 2 .
If A 2 A 1 = b + c a where a , b , c ∈ N and g cd ( a , b , c ) = 1 , enter answer as a 2 + b 2 + c 2 .
Try similar problems
- Ellipse's Circumscribed Perimeter
- Highly Elliptical Area
- Areal Parabolic Centroid
- Co-Normal Parabolic Centroid
All of my problems are original
The answer is 50.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Aryan Sanghi a very nice problem and solution. Thanks for posting. Upvoted
Log in to reply
Thanku for appreciation. :)
@Aryan Sanghi , you can align the equal sign = using \begin{align} \end{align}. Note that double backslash \ \ is to go to next line.
Log in to reply
@Chew-Seong Cheong I didn't understand, the application?
Log in to reply
They are LaTex codes. I have used them to align the equal sign = 's after A 2 A 1 in Aryan's solution.
Ohk, I didn't knew it. I'll definitely use it from next solution. :)
Log in to reply
You can size your image by adding after jpg "|width=400". The large the number, for example 500, the larger the image. Check the image in your solution. For the problem, I added width=300.
You must align with &
Interestingly, the ellipse that satisfies the conditions is φ 2 x 2 + y 2 = 1 , where the major axis a = φ = 2 1 + 5 is the golden ratio and the minor axis b = 1 or an eccentricity e = φ 1 (see proof below). Then the radius of the two circle is r = e = φ 1 . Then A 2 A 1 = π a b 2 π r 2 = φ 2 2 = ( 2 1 + 5 ) 2 2 = 2 5 + 6 8 = 5 + 3 4 . Therefore a 2 + b 2 + c 2 = 4 2 + 5 2 + 3 2 = 5 0 . (Note that a and b are not major and minor axes.)
Proof: Let the ellipse be a 2 x 2 + b 2 y 2 = 1 with foci F 1 ( − c , 0 ) and F 2 ( c , 0 ) , where c = a 2 − b 2 .
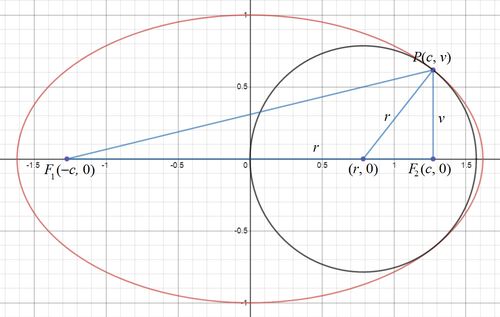
Note that latus rectum is the straight line passes through a focus and perpendicular ot the major axis. Let the top end of the latus rectum through F 2 be P ( c , v ) . By definition of ellipse F 1 P + F 2 P = 2 a or
4 c 2 + v 2 + v 4 c 2 + v 2 4 c 2 + v 2 ⟹ v = 2 a = 2 a − v = 4 a 2 − 4 a v + v 2 = a a 2 − c 2 = a b 2
The gradient at a point on the ellipse is given by d x d y = − a 2 y b 2 x . At P ( c , v ) , we have d x d y ∣ ∣ ∣ ∣ x = c = − a 2 v b 2 c = − a c . Let the radius of the circles be r . Then the circle for x ≥ 0 is ( x − r ) 2 + y 2 = r 2 and d x d y = − y x − r . At P ( c , v ) , d x d y ∣ ∣ ∣ ∣ x = c = − v c − r . Since the circle and ellipse are tangent at P , then
v c − r b 2 a ( c − r ) c − r r = a c = a c = a 2 b 2 c = c ( 1 − a 2 b 2 ) = a 2 c 3
For the circle at P :
( c − r ) 2 + v 2 c 2 − 2 c r + r 2 + a 2 b 4 c 2 − a 2 2 c 4 + a 2 b 4 a 2 c 2 − 2 c 4 + b 4 a 2 ( a 2 − b 2 ) − 2 ( a 4 − 2 a 2 b 2 + b 4 ) + b 4 a 4 − 3 a 2 b 2 + b 4 = r 2 = r 2 = 0 = 0 = 0 = 0
a 2 ⟹ a = 2 3 b 2 + 9 b 4 − 4 b 4 = 2 3 + 5 b 2 = φ b Note that φ 2 = ( 2 1 + 5 ) 2 = 2 3 + 5
Putting b = 1 , ⟹ a = φ , c = φ 2 − 1 = φ + 1 − 1 = φ , and r = a 2 c 3 = φ 1 .
Excellent solution sir. Thanku for sharing it with us. :)
Log in to reply
Nice problem.
Let's solve it using coordinate geometry
Let the equation of ellipse be a 2 x 2 + b 2 y 2 = 1 where a > b . Let eccentricity of ellipse be e .
Now, let the parametric coordinates of points on ellipse be ( a cos θ , b sin θ ) .
Now, coordinates of endpoints of latus rectum are ( a e , a b 2 ) and ( a e , − a b 2 ) . Comparing with polar coordinates we get cos θ = e and sin θ = ± 1 − e 2
Now, equation of normal at point ( a cos θ , b sin θ ) is cos θ a x − sin θ b y = a 2 − b 2
So, equations of normals at endpoints of latus rectum are
e a x − 1 − e 2 b y = a 2 − b 2 and e a x + 1 − e 2 b y = a 2 − b 2
Now the normals will intersect at circle's center C ( h , k ) . Solving, we get
h = e a a 2 − b 2 and k = 0
Now, b 2 = a 2 ( 1 − e 2 ) , so
h = a e 3 and k = 0
Now, as circle touches minor axis, i.e. y-axis, so
radius of circle = x-coordinate of center
radius of circle = a e 3
Now, radius of circle = distance between center of circle and ends of latus rectum
a e 3 = ( a e 3 − a e ) 2 + ( a b 2 ) 2
a e 3 = ( a e 3 − a e ) 2 + ( a ( 1 − e 2 ) ) 2
a 2 e 6 = a 2 e 6 − 2 a 2 e 4 + a 2 e 2 + a 2 − 2 a 2 e 2 + a 2 e 4
e 4 + e 2 − 1 = 0
e 2 = 2 5 − 1
Now, area of circles A 1 = 2 × ( π ( a e 3 ) 2 ) = 2 π a 2 e 6 and area of ellipse A 2 = π a b = π a 2 1 − e 2
A 2 A 1 = π a 2 1 − e 2 2 π a 2 e 6 = 1 − e 2 2 e 6 = 1 − 2 5 − 1 2 ( 2 5 − 1 ) 3 = 2 4 6 − 2 5 5 − 2 = 4 5 − 1 5 − 2 = 3 + 5 4
So, a = 4 , b = 5 , c = 3 , a 2 + b 2 + c 2 = 5 0
Visualisation: Area of circles is about 7 6 . 3 9 3 % of ellipse's area