Ellipse's Circumscribed Perimeter
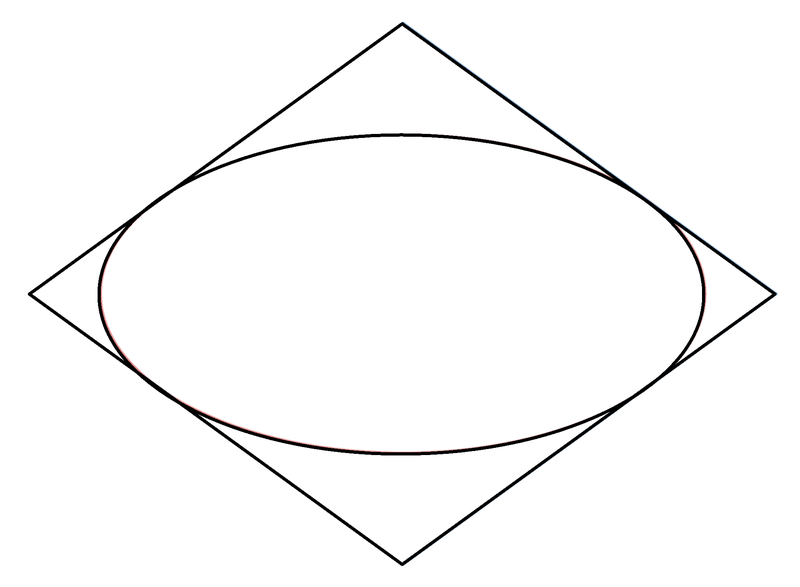
Around an ellipse of eccentricity e = 0 . 8 5 circumscribe a quadrilateral with minimum perimeter and vertices on the major and minor axes of the ellipse.
If the area of the ellipse is A 1 and the area of the quadrilateral is A 2 , find A 2 A 1 × 1 0 0 .
Try similar problems
All of my problems are original .
The answer is 74.672.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
You should use Geogebra for better diagrams :)
Log in to reply
I don't know how to use it. 😅
Btw, how was the question? :)
@Siddharth Chakravarty , @Aryan Sanghi .Have a look at this
When you are using A 2 A 1 , you don't have to "fixed" the ellipse. Because A 1 and A 2 will proportionate accordingly. Please do not provide links to every math term. It is disruptive to read and the reader may think that you think they know nothing. This is a problem question not a wiki where you provide reference with a link for every relevant term. Try to be as simple as possible not as long as you can write. Like a paragraph to explain A 2 A 1 × 1 0 0 in bold. I have amended the problem statement for you as above. I know that you like to set problem but do check with other problems to see the standard required. Also learn up a graphic application. I use Desmos for the above remove the grips and axis through settings and print screen to transfer to Paint to place in the problem question.
Log in to reply
Ok, I'll definitely follow the guidelines sir. Also, I'll try using desmos whenever I can. :)
By differentiating the ellipse equation a 2 x 2 + b 2 y 2 = 1 we get a 2 2 x d x + b 2 2 y d y = 0 and hence d x d y = − a 2 b 2 y x Now suppose the line segment in the first quadrant is tangent at the point (x,y), then it will intersect the y-axis at x + c and the x-axis at y + d where c = − y d y d x = b 2 x a 2 y 2 and d = − x d x d y = a 2 y b 2 x 2 .
If s is the length of our line segment then we have s 2 = ( y + a 2 y b 2 x 2 ) 2 + ( x + b 2 x a 2 y 2 ) 2 which is rewritten as s 2 = ( y 2 a 4 1 + x 2 b 4 1 ) ( a 2 y 2 + b 2 x 2 ) 2
Using the ellipse equation we can substitute a 2 y 2 = b 2 ( a 2 − x 2 ) , so that s 2 = ( a 2 b 2 ( a 2 − x 2 ) 1 + x 2 b 4 1 ) ( b 2 a 2 ) 2
At minimum value for s we must have that d x d s 2 = 0 , from which it follows that a 2 ( a 2 − x 2 ) = b 2 x 2
Now we use the relationship b 2 = ( 1 − e 2 ) a 2 to get e 2 x 4 − 2 a 2 x 2 + a 4 = 0 which is a quadratic in x 2 that has roots x 2 = e 2 a 2 ( 1 ± 1 − e 2 ) . We discard the root with ∣ x ∣ > a , so that a x = e 1 1 − 1 − e 2 Hence we also find b y = e 1 e 2 − 1 + 1 − e 2 a c = x a b 2 y 2 = e 1 − 1 − e 2 e 2 − 1 + 1 − e 2 b d = y b a 2 x 2 = e e 2 − 1 + 1 − e 2 1 − 1 − e 2
The area ratio can now be written as 4 × 2 1 ( x + c ) ( y + d ) π a b = 2 π x + c a y + d b = 2 π e 1 − 1 − e 2 e e 2 − 1 + 1 − e 2 = 2 π 1 + 1 − e 2 4 1 − e 2
Nice solution sir. Thanku for sharing it with us. :)
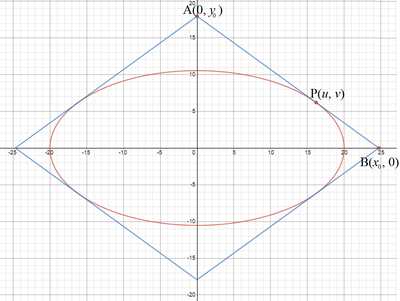
Let solve this problem for a general case of a 2 x 2 + b 2 y 2 = 1 , where a and b are the major semiaxis and minor semiaxis respectively. The gradient of a point on an ellipse is given by differentiating the equation on both sides with respect to x , a 2 2 x + b 2 2 y ⋅ d x d y = 0 ⟹ d x d y = − a 2 y b 2 x .
Let a side of the quadrilateral A B tangent to the ellipse at P ( u , v ) . Then we have x − u y − v = − a 2 v b 2 u . Let A ( 0 , y 0 ) and B ( x 0 , 0 ) . Then − u y 0 − v = − a 2 v b 2 u ⟹ y 0 = a 2 v b 2 u 2 + v = v b 2 ( a 2 u 2 + b 2 v 2 1 ) = v b 2 . Similarly, x 0 = u a 2 . Let u = a cos θ and v = b sin θ . Then x 0 = cos θ a and y 0 = sin θ b .
Let the length A B = ℓ . Then the perimeter of quadrilateral is 4 ℓ . The perimeter is shortest when ℓ is shortest or ℓ 2 is the minimum. Then we have:
ℓ 2 d θ d ℓ 2 cos 3 θ a 2 sin θ tan 4 θ ⟹ tan θ = x 0 2 + y 0 2 = cos 2 θ a 2 + sin 2 θ b 2 = cos 3 θ a 2 sin θ − sin 3 θ b 2 cos θ = sin 3 θ b 2 cos θ = a 2 b 2 = a b Differentiate both sides w.r.t. θ Putting d θ d ℓ 2 = 0 ⟹ sin θ = a + b b , cos θ = a + b a
Since d x 2 d 2 ℓ 2 > 0 , when θ = tan − 1 a b , therefore ℓ is minimum when θ = tan − 1 a b . Then x 0 = cos θ a = a ( a + b ) and y 0 = sin θ b = b ( a + b ) . And A 2 = 2 x 0 y 0 = 2 ( a + b ) a b . Since A 1 = π a b , then A 2 A 1 × 1 0 0 = a + b 5 0 π a b .
For eccentricity e = 0 . 8 5 = 2 0 1 7 = 1 − a 2 b 2 .. ⟹ a 2 b 2 = 1 − e 2 = 4 0 0 1 1 1 , ⟹ a = 2 0 , b = 1 1 1 and A 2 A 1 × 1 0 0 = 2 0 + 1 1 1 5 0 π 2 0 1 1 1 ≈ 7 4 . 7 .
Nice solution sir. Thanku for sharing it with us. :) Also, thanku for Posting a good diagram in question sir. :)
Lets solve it using coordinate geometry
Let equation of ellipse be a 2 x 2 + b 2 y 2 = 1
Let tangent be drawn at point P ( a cos θ , b sin θ )
Equation of tangent at P is
a x cos θ + b y sin θ = 1
It intersects the major and minor at C ( a sec θ , 0 ) and B ( 0 , b cosec θ )
Length of B C is
L = a 2 sec 2 θ + b 2 cosec 2 θ
To minimise L , d θ d L = 0
d θ d L = 2 a 2 sec 2 θ + b 2 csc 2 θ 2 a 2 sec 2 θ tan θ − 2 b 2 cosec 2 θ cot θ = 0
a 2 b 2 = tan 4 θ or tan 2 θ = a b
sec θ = a a + b and cosec θ = b a + b
Now, perimeter will be minimum when all sides are of this length L m i n = a 2 sec 2 θ + b 2 cosec 2 θ = a + b
So, area of quadrilateral is
A 2 = 4 × 2 1 ( a sec θ ) ( b cosec θ )
A 2 = 2 a b a b a + b
A 2 = 2 a b ( a + b )
Now, Area of ellipse is A 1 = π a b
So,
A 2 A 1 = 2 a b ( a + b ) π a b
A 2 A 1 = 2 ( a b + b a ) π
Now, e 2 = 1 − a 2 b 2 or a b = 4 1 − e 2
Therefore,
A 2 A 1 = 2 ( 4 1 − e 2 + 4 1 − e 2 1 ) π
Putting e = 0 . 8 5 , we get
A 2 A 1 = 2 ( 4 1 − 0 . 8 5 2 + 4 1 − 0 . 8 5 2 1 ) π
A 2 A 1 = 0 . 7 4 6 7 2
A 2 A 1 × 1 0 0 = 7 4 . 6 7 2
Therefore, area of ellipse A 1 is 7 4 . 6 7 2 % of area of quadrilateral A 2 .
Fun fact(or bonus question): minimum area of quadrilateral gives area of ellipse as 2 5 π = 7 8 . 5 3 8 % of quadrilateral's area. Can you prove it?