Elliptical Area Under the Cutting Line

Calculus Level 5

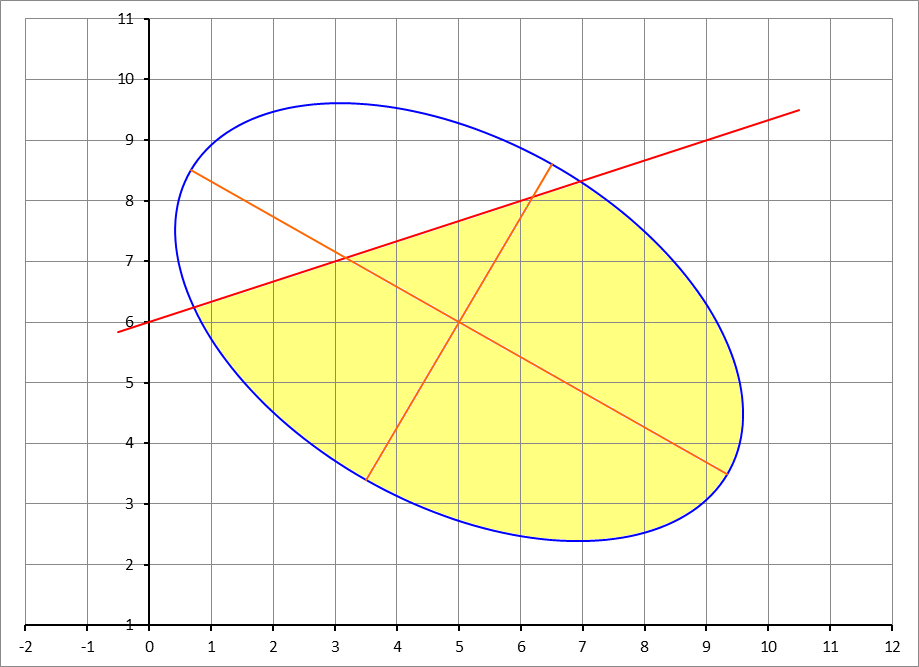
An ellipse is centered at $(5, 6)$ . It has a semi-minor axis of 3 units, and a semi-major axis of 5 units. The semi-minor axis makes an angle of $60^{\circ}$ with the $x$ -axis, and the semi-major axis makes an angle of $60^{\circ}$ with the $y$ -axis, as shown in the figure above. A line whose equation is given by

$y = \dfrac{1}{3} x + 6$

cuts through the ellipse. Find the area of the region bounded by the ellipse that lies under the line. (Shaded area in the figure).

Round your answer to two decimal places.

The answer is 34.49.

1 solution

Hosam Hajjir
Jul 29, 2016

The ellipse can be represented in parametric form as

$r(t) = r_c + v_1 \cos(t) + v_2 \sin(t)$

where $r_c = [5, 6 ,0 ]^T, v_1 = R [3, 0,0]^T, v_2 = R [0, 5, 0]^T$

with $R$ being the rotation matrix by $60^{\circ}$ or $\pi / 3$

That is,

$R = \begin{bmatrix} \cos \frac{\pi}{3} && -\sin \frac{\pi}{3} && 0 \\ \sin \frac{\pi}{3} && \cos \frac{\pi}{3} && 0 \\ 0 && 0 && 1 \end{bmatrix}$

Using the x-component and y-component of $r(t)$ , we impose the condition

$y \le \frac{1}{3} x + 6$

This results in a range for $t$ in the form $[t_1, t_2 ]$ . To find the area, we perform the following integral

$A = \frac{1}{2} \| \int_{t_1}^{t_2} r(t) \times \frac{dr}{dt} dt + r(t_2) \times r(t_1) \|$

Elliptical Area Under the Cutting Line

The answer is 34.49.

1 solution

0 pending reports