Elliptical disc in the corner
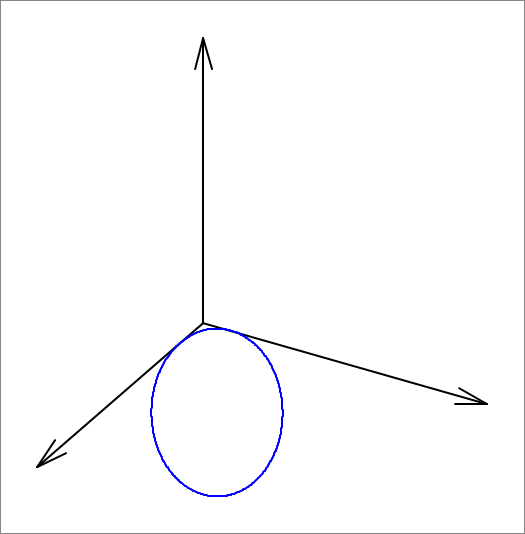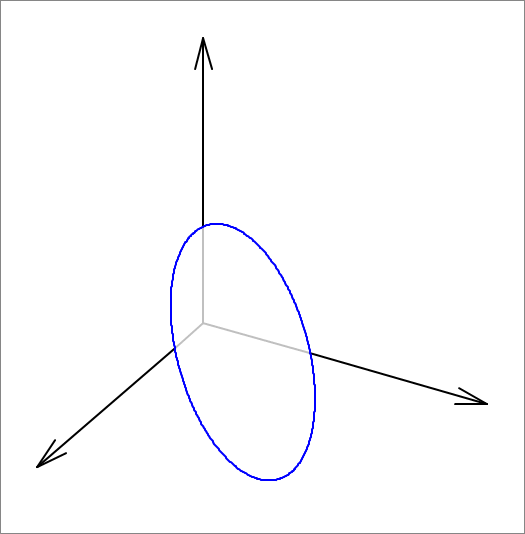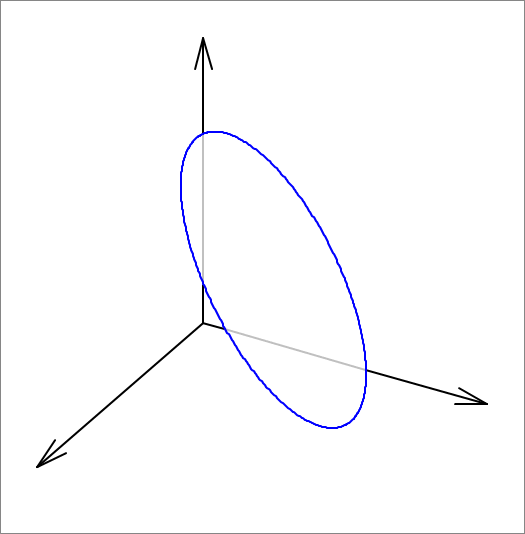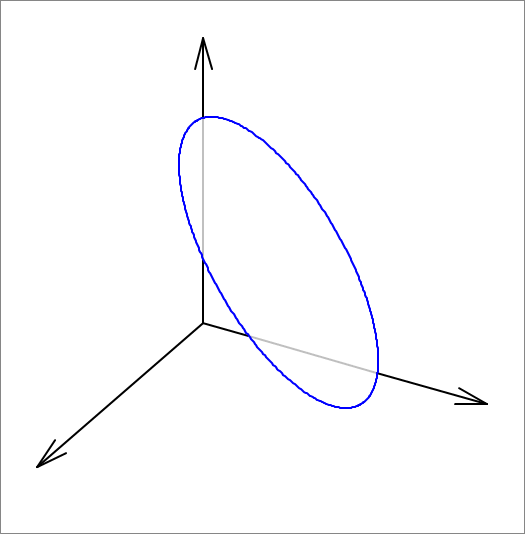
An elliptical disc has a semi-major axis length of 5 and a semi-minor axis length of 2 . It is pushed against the corner of the first octant (where x ≥ 0 , y ≥ 0 and z ≥ 0 ). The elliptical disc cannot penetrate the coordinate planes (the x y , x z , and y z planes), and can only be tangent to them. In its final position, the unit normal to its plane is given by ( sin 3 π cos 6 π , sin 3 π sin 6 π , cos 3 π ) . The elliptical disc is oriented in such a way that its major axis makes an angle of + 6 π (counterclockwise) with the direction of the steepest descent on its plane. There are three tangency points with the three coordinate planes. If ( 0 , a , b ) is the tangency point with the y z plane, then find a + b .
The answer is 9.453.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
You've done it again. Excellent Work.
The unit normal specified by the problem is
n ^ = ( sin θ cos ϕ , sin θ sin ϕ , cos θ )
where θ = 3 π and ϕ = 6 π . The unit vector in the direction of the steepest descent is given by,
u ^ 1 = ( cos θ cos ϕ , cos θ sin ϕ , − sin θ )
In addition, let
u ^ 2 = ( − sin ϕ , cos ϕ , 0 )
Then the three unit vectors u ^ 1 , u ^ 2 and n ^ make a right-handed reference frame.
The major axis of the ellipse makes an angle of ψ = 6 π with u ^ 1 . Thus, it is along the unit vector w ^ 1 , and the minor axis is along w ^ 2 , where
[ w ^ 1 , w ^ 2 ] = [ u ^ 1 , u ^ 2 ] R ( 6 π )
and where,
R ( 6 π ) = [ cos 6 π sin 6 π − sin 6 π cos 6 π ]
Now the points on the perimeter of the ellipse can be parameterized as:
r ( t ) = r C + a cos t w ^ 1 + b sin t w ^ 2
where a = 5 is the semi-major axis length and b = 2 is the semi-minor axis length, and where r C = ( x C , y C , z C ) is the position vector of the center of the ellipse. Tangency to the three coordinate planes implies that, for the x y plane, we're looking for t 1 ∈ [ 0 , 2 π ) , such that,
0 = z C + a cos t 1 w 1 z + b sin t 1 w 2 z
We also require that d t d r has a zero z -component at t = t 1 , that is,
0 = − a sin t 1 w 1 z + b cos t 1 w 2 z
The last equation can be solved quite easily for two possible values of t 1 that are separated by π .
To choose the correct one, we use the fact that z C is positive, and after some trigonometry, we deduce that,
z C = a 2 w 1 z 2 + b 2 w 2 z 2
Similar formulas apply to x C and y C . Finally, to find the tangency point with the y z plane, we simply plug in
the value of t 3 into the parametric equation of the ellipse.
r ∗ = r C + a cos t 3 w ^ 1 + b sin t 3 w ^ 2
where, − a sin t 3 w 1 x + b cos t 3 w 2 x = 0
And this gives the required result, r ∗ = ( 0 , 3 . 1 9 8 2 5 , 6 . 2 5 4 9 3 ) making the answer ( 3 . 1 9 8 2 5 + 6 . 2 5 4 9 3 ) = 9 . 4 5 3 1 8
The elliptical disc is tangent to the three sides of the triangle formed by the extension of the plane that is on the x y , x z , and y z planes:
Since the unit normal vector to the plane of the disc is ( sin 3 π cos 6 π , sin 3 π sin 6 π , cos 3 π ) = ( 4 3 , 4 3 , 2 1 ) , the equation of the plane is 4 3 x + 4 3 y + 2 1 z = d , and its x -, y -, and z -intercepts ( A , B , and C ) solve to ( 3 4 d , 0 , 0 ) , ( 0 , 3 4 d , 0 ) , and ( 0 , 0 , 2 d ) , which by Pythagorean's Theorem makes the sides of the triangle 3 8 d , 3 2 2 1 d , and 3 2 1 3 d .
Now move △ A B C to a Cartesian coordinate system with A at ( 0 , 0 ) and B at ( 3 8 d , 0 ) :
C is 3 2 1 3 d away from A so by the distance formula C x 2 + C y 2 = 3 2 1 3 d , and C is 3 2 2 1 d away from B so ( C x − 3 8 d ) 2 + C y 2 = 3 2 2 1 d , and this solves to ( C x , C y ) = ( 3 2 d , 3 4 d ) . This means the equation of the line A C is y = 2 3 x and the equation of the line B C is y = − 3 2 ( x − 3 8 d ) .
The steepest descent of the plane is the altitude of △ A B C , so the ellipse is rotated 6 π counterclockwise from the vertical. Since the semi-major axis is 5 and the semi-minor axis is 2 , the equation of the ellipse before the rotation is 4 ( x − h ) 2 + 2 5 ( y − k ) 2 = 1 for center ( h , k ) , and is 4 0 0 7 9 ( x − h ) 2 + 2 0 0 2 1 3 ( x − h ) ( y − k ) + 4 0 0 3 7 ( y − k ) 2 = 1 after the rotation. Using implicit differentiation, the slope at any point on the ellipse solves to m = 2 1 3 ( x − h ) + 3 7 ( y − k ) − 7 9 ( x − h ) − 2 1 3 ( y − k ) .
The ellipse is tangent to y = 0 which has a slope of m = 0 at y = 0 . Then 4 0 0 7 9 ( x − h ) 2 + 2 0 0 2 1 3 ( x − h ) ( y − k ) + 4 0 0 3 7 ( y − k ) 2 = 1 and m = 2 1 3 ( x − h ) + 3 7 ( y − k ) − 7 9 ( x − h ) − 2 1 3 ( y − k ) with m = 0 and y = 0 solves to k = 2 7 9 .
The ellipse is also tangent to y = 2 3 x which has a slope of m = 2 3 . Then 4 0 0 7 9 ( x − h ) 2 + 2 0 0 2 1 3 ( x − h ) ( y − k ) + 4 0 0 3 7 ( y − k ) 2 = 1 and m = 2 1 3 ( x − h ) + 3 7 ( y − k ) − 7 9 ( x − h ) − 2 1 3 ( y − k ) with k = 2 7 9 , m = 2 3 , and y = 2 3 x solves to h = 1 2 1 ( 5 9 3 + 2 3 7 ) .
The ellipse is also tangent to y = − 3 2 ( x − 3 8 d ) which has a slope of m = − 3 2 at T . Then 4 0 0 7 9 ( x − h ) 2 + 2 0 0 2 1 3 ( x − h ) ( y − k ) + 4 0 0 3 7 ( y − k ) 2 = 1 and m = 2 1 3 ( x − h ) + 3 7 ( y − k ) − 7 9 ( x − h ) − 2 1 3 ( y − k ) with k = 2 7 9 , h = 1 2 1 ( 5 9 3 + 2 3 7 ) , m = − 3 2 and y = − 3 2 ( x − 3 8 d ) solves to x = T x = 2 3 1 1 + 1 2 5 9 3 + 1 2 2 3 7 , y = T y = 2 1 3 3 3 7 3 + 2 7 9 , and d = 3 2 1 ( 5 9 3 + 3 1 3 3 + 4 2 3 7 ) . We now know the coordinates of B are ( 1 2 1 ( 5 9 3 + 3 1 3 3 + 4 2 3 7 ) , 0 ) , and by the distance formula, B T 2 = 1 5 2 1 ( 7 3 0 7 + 3 7 3 1 5 2 1 ) .
Moving back to the three-dimensional picture, the equation of the line B C is z = 2 3 y + 2 d . Since T is on B C , T z = 2 3 T y + 2 d and by the distance formula ( T y − 3 4 d ) 2 + T z 2 = B T 2 , and since d = 3 2 1 ( 5 9 3 + 3 1 3 3 + 4 2 3 7 ) and B T 2 = 1 5 2 1 ( 7 3 0 7 + 3 7 3 1 5 2 1 ) , this solves numerically to ( T y , T z ) ≈ ( 3 . 1 9 8 , 6 . 2 5 5 ) .
Therefore, a = T y ≈ 3 . 1 9 8 and b = T z ≈ 6 . 2 5 5 , and a + b ≈ 3 . 1 9 3 + 6 . 2 5 5 ≈ 9 . 4 5 3 .