Elliptical Distances
Consider the point P ( − 1 , 0 ) on the ellipse given by the equation 4 x 2 + y 2 = 4 . There are two points ( a , b ) and ( a , c ) on the ellipse whose distance from P is a maximum. What is the value of a ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
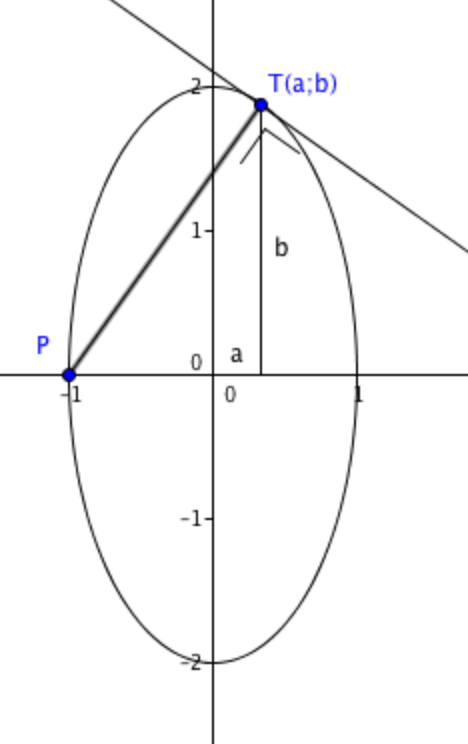
To be a maximum, the tangent at T must be perpendicular to P T .
Slope of the tangent at point ( x ; y ) : ( 4 x 2 + y 2 ) ′ = 4 ′ ⇒ 8 x + 2 y y ′ = 0 ⇔ y ′ = y − 4 x . At T , it is b − 4 a .
Slope of P T is a + 1 b .
The lines are perpendicular ⇔ the product of their slope is − 1 : b − 4 a ⋅ a + 1 b = − 1 ⇒ 4 a = a + 1 ⇔ a = 3 1 .
Very nice solution
Let ( x , y ) be a point on the ellipse. The distance between ( x , y ) and the given point ( − 1 , 0 ) is given by ( x + 1 ) 2 + y 2
Using the fact that 4 x 2 + y 2 = 4 → y 2 = 4 − 4 x 2 , we rewrite the distance above as ( x + 1 ) 2 + ( 4 − 4 x 2 ) → − 3 x 2 + 2 x + 5
This quantity is maximized when the quadratic inside the radical uses x = − 2 a b = 3 1 .