Elliptical section of a right circular cone by HCR
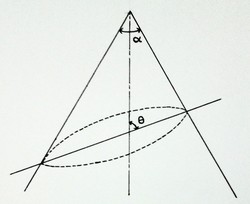 A right circular cone, with apex angle
, is thoroughly cut with a smooth plane inclined at an acute angle
with the geometrical axis to generate an elliptical section. (As shown in the above diagram). Find the eccentricity of elliptical section generated.
A right circular cone, with apex angle
, is thoroughly cut with a smooth plane inclined at an acute angle
with the geometrical axis to generate an elliptical section. (As shown in the above diagram). Find the eccentricity of elliptical section generated.
The answer is 0.577350269.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
In general, eccentricity ( e ) of elliptical section generated is given by following formula
e = cos 2 α cos θ
∴ e = cos 3 0 ∘ cos 6 0 ∘ = 3 / 2 1 / 2 = 1 / 3 = 0 . 5 7 7 3 5 0 2 6 9