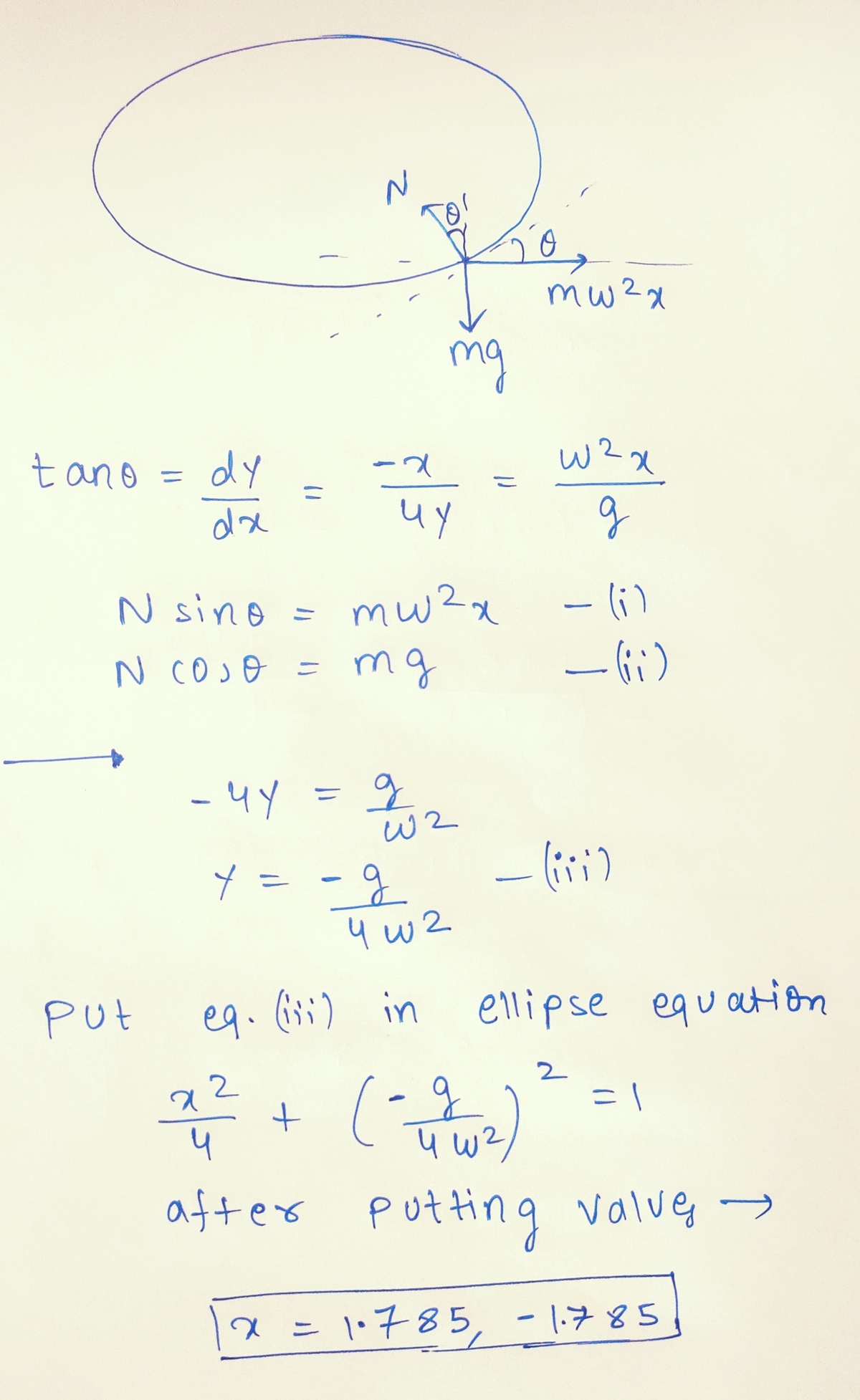Elliptical Tachometer

Classical Mechanics Level 4

There is a bead attached to a smooth wire in the shape of the following elliptical curve. The bead is confined to the wire, but can slide along it freely.

x 2 4 + y 2 1 = 1 \large{\frac{x^2}{4} + \frac{y^2}{1} = 1}

The wire rotates around the y y -axis with constant angular speed ω \omega . If the bead maintains a constant distance D D from the y y -axis, what is ⌊ 1000 D ⌋ \lfloor 1000 \, D \rfloor ?

Details and Assumptions:
1) Bead mass m = 1 kg m = 1 \, \text{kg}
2) Gravity g = 10 m/s 2 g = 10 \, \text{m/s}^2 in the − y -y direction
3) Angular speed ω = 3 4 π rad/s \omega = \frac{3}{4} \pi \,\, \text{rad/s}
4) ⌊ ⋅ ⌋ \lfloor \cdot \rfloor denotes the "floor" function


The answer is 1785.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Nj Star
Feb 13, 2020

1 Helpful 1 Interesting 1 Brilliant 0 Confused
Laszlo Mihaly
Nov 12, 2018

In a rotating system of reference there are two contributions to the potential energy: the gravitational potential, V g = m g y V_g=mgy and the centrifugal potential, V c = 1 2 m ω 2 r 2 = 1 2 m ω 2 x 2 V_c=\frac{1}{2} m\omega^2 r^2=\frac{1}{2} m\omega^2 x^2 . The condition for equilibrium is d V / d x = 0 dV/dx=0 . If we express y y as y = b 1 − ( x / a ) 2 y=b\sqrt{1-(x/a)^2} , we get

m ω 2 x = m g b a 2 x 1 − x 2 / a 2 m\omega^2 x = mg \frac{b}{a^2}\frac{x}{\sqrt{1-x^2/a^2}}

where a = 2 a=2 meter and b = 1 b=1 meter. Solving this for x x we get x = a 1 − ( g b ω 2 a 2 ) 2 = 1.785 x=a\sqrt{1-\left(\frac{gb}{\omega^2 a^2}\right)^2}=1.785 m

2 Helpful 0 Interesting 0 Brilliant 2 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...