Elongation in rod
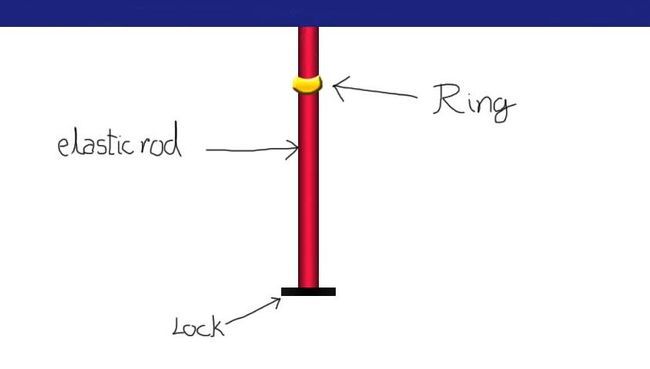 An elastic rod of costant
and length
is hung at a point P, rod have a massless lock at the other end. A smooth ring of mass
falls from P (It is the same point from where the rod was hung), find the max elongation in the rod.
An elastic rod of costant
and length
is hung at a point P, rod have a massless lock at the other end. A smooth ring of mass
falls from P (It is the same point from where the rod was hung), find the max elongation in the rod.
Details and Asumptions :
-
Gravity acts vertically downwards.
-
Position of ring in picture is not of initial position.
-
Length l is taken from point P to lock.
-
-
All the values above are in SI units
The answer is 60.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We can easily use conservation of energy here.
From the figure
Initial energy of the system= m g l
Final energy of the system= 2 k x 2 − m g x
By conservation of energy
m g l = 2 k x 2 − m g x
On putting values we get
x 2 − 4 0 x − 1 2 0 0 = 0 So x = 6 0