EM Orbit

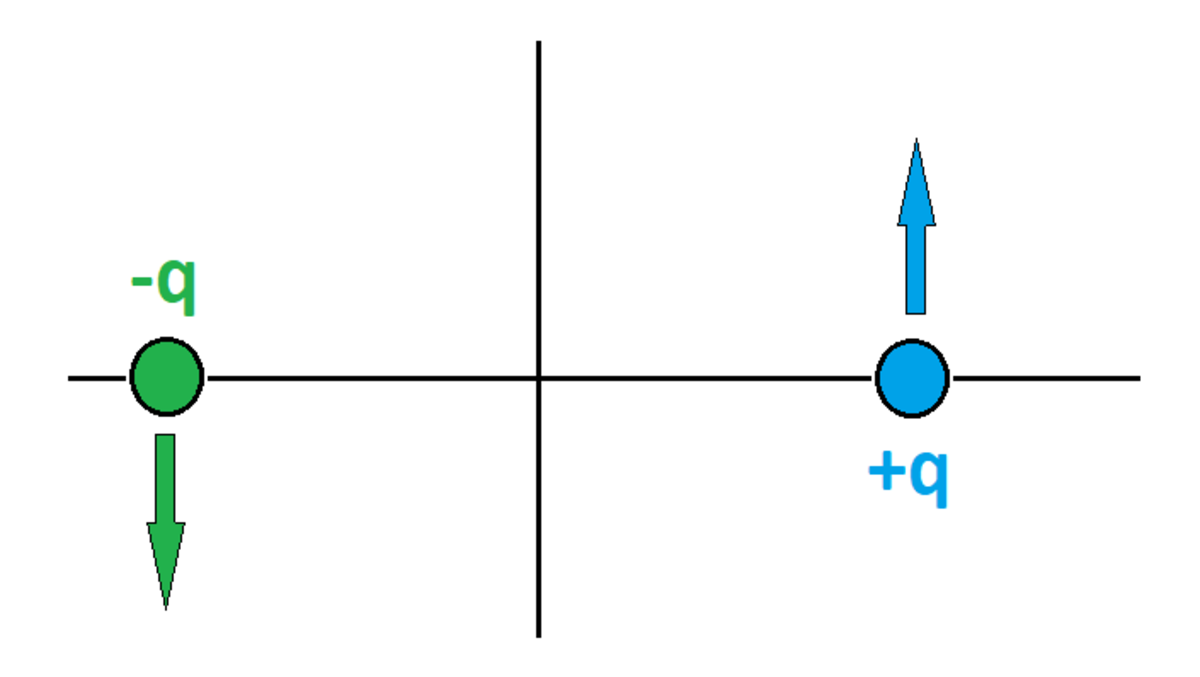
Electricity and Magnetism Level pending

Particle 1 1 has mass m m and charge + q +q , and Particle 2 2 has mass m m and charge − q -q . At a particular time, Particle 1 1 is at position ( x , y ) = ( 1 , 0 ) (x,y) = (1,0) with speed v v in the + y +y direction. At the same time, Particle 2 2 is at position ( x , y ) = ( − 1 , 0 ) (x,y) = (-1,0) with speed v v in the − y -y direction.

If the particles both maintain uniform circular motion around the origin, what is the value of v v ? Be sure to read the "Details and Assumptions" carefully.

Details and Assumptions:
1) Each particle exerts both an electric and a magnetic influence on the other
2) The magnetic flux density calculation is described in this link
3) m = 1 m = 1
4) q = 6 q = 6
5) Permittivity and permeability ϵ 0 = μ 0 = 1 \epsilon_0 = \mu_0 = 1
6) I think this approach is still ultimately wrong, since accelerating charged particles are supposed to lose energy due to emission of electromagnetic radiation. But that will be a subject for another time. For the purposes of this problem, consider electric and magnetic forces but neglect electromagnetic radiation.


The answer is 1.5886.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Post a problem in which particle lose energy due to emission of electromagnetic radiation.

Due to a moving charge magnetic field B ⃗ \vec{B} is generated as B ⃗ = μ 0 4 π q v ⃗ × r ⃗ r 3 \textcolor{#20A900}{\vec{B}=\frac{\mu_{0}}{4π} \frac{q\vec{v}×\vec{r}}{r^{3}}} Using this the magnetic field on − q -q comes B − q ⃗ = μ 0 4 π q v r 2 ( − k ⃗ ) \vec{B_{-q}}=\frac{\mu_0}{4π}\frac{qv}{r^{2}}(\vec{-k}) B ⃗ = 3 v 8 π ( − k ⃗ ) \vec{B}=\frac{3v}{8π}(\vec{-k})
Force on a particle moving in magnetic field F ⃗ = q ( v ⃗ × B ⃗ ) \textcolor{#20A900}{\vec{F}=q(\vec{v}×\vec{B})}
In the − q -q , F m F_m (magnetic force) will be in + x +x direction
Of magnitude F m ⃗ = 9 v 2 4 π i ⃗ \vec{F_m}=\frac{9v^{2}}{4π} \vec{i}
And while calculating electric force using coulomb's law F c ⃗ = k q 1 q 2 r ⃗ r 3 \vec{F_c}=\frac{kq_{1}q_{2}\vec{r}}{r^{3}} As the charges are unlike force will be attractive. F e ⃗ = 9 4 π i ⃗ \vec{F_e}=\frac{9}{4π}\vec{i}
F m a g n e t i c ⃗ + F e l e c t r i c ⃗ = F c e n t r i p e t a l ⃗ \vec{F_{magnetic}}+\vec{F_{electric}}=\vec{F_{centripetal}}
9 v 2 4 π + 9 4 π = v 2 1 \frac{9v^{2}}{4π}+\frac{9}{4π}=\frac{v^{2}}{1}
v ⃗ ≈ 1.5886 ( − j ⃗ ) \textcolor{#3D99F6}{\boxed{\vec{v} \approx 1. 5886(\vec{-j})}}


2 Helpful 2 Interesting 2 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...