Embed the Square

If we fold the four red flaps inward, they enclose a square with sides of length 2 without overlapping. The original gray square has length $2 + \sqrt 2$ . Therefore $A = (2 + \sqrt 2)^2 - 2^2 = 4\sqrt 2 + 2 \approx \boxed{7.657}.$

Each trapezoid consists of two triangles and a rectangle. Because a regular octagon has angles of $135^\circ$ , we can drop a perpendicular from one of the octagon's vertices, creating a $45-45-90$ right triangle.

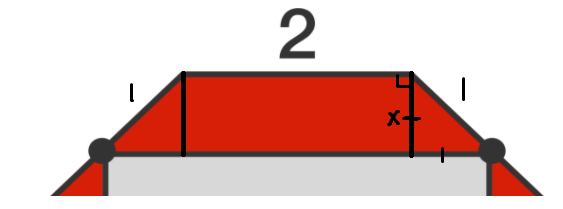
Since this right triangle must be isosceles, from Pythagorean Theorem we can find that $x=\frac{1}{\sqrt{2}}$ . Therefore, the triangle has area $\frac{1}{2}\times\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2}}=\frac{1}{4}$ . The same logic can be applied to the left triangle. The rectangle has area $2\times\frac{1}{\sqrt{2}}=\sqrt{2}$ . There are $8$ total triangles and $4$ total rectangles in the entire image, so the red area is $8\times\frac{1}{4}+4\sqrt{2}\approx \boxed{7.656854}$ .

To find the area of one of the trapezoids, we can use the formula $a = \frac {b_1 + b_2}{2} \times h$ . We know that the length of one of the bases is 2, and we can find the other by finding the area of the triangles on the corners of the trapezoid and then add the value to the top bases length.

To find the area of the corner triangles, we need to prove that the triangle is a 45-45-90 triangle. The bases of trapezoids are parallel, so we know the line that forms the right triangle is also perpendicular to the top base. The measures of the interior angles of a regular octagon is $135 ^ \circ$ , so the measure of the angles of the triangle is $135 ^ \circ - 90 ^ \circ = 45 ^ \circ$ . Therefore, we have a 45-45-90 triangle.

For a 45-45-90 triangle, the legs have a measure of $x$ while the hypotenuse has a measure of $x \sqrt{2}$ . Plugging in 1 as the hypotenuse, we can find the value for the legs: $1 = x \sqrt{2}, x = \frac{1}{\sqrt{2}}$

Now we can find the areas of the trapezoids’ second bases, which has the measure of the first base plus the length of the 2 bottom legs of the right triangle, so $b_2 = 2 + \frac{2}{\sqrt{2}}$ .

There are four trapezoids so we multiply the area by four. Therefore, our answer is:

$a = 4 \times \frac{b1 + b2}{2} \times h$

$a = 4 \times \frac{2 + 2 + \frac{2}{\sqrt{2}}}{2} \times \frac{1}{\sqrt{2}}$

$a = \frac{16 + \frac{8}{\sqrt{2}}}{2}$ $\times \frac{1}{\sqrt{2}}$

$a = \frac{16 + \frac{8}{\sqrt{2}}}{2 \sqrt{2}} \approx$ 7.657

As a regular octagon is a square with triangles removed and these right angle isosceles triangles are half a square that makes the invisible triangle sides 2^1/2 = 1.4142... (Pythagoras, extra digit for accuracy to three decimal places) And then the big square encompassing the octagon has a side of length 1.4142+2+1.4142 = 4.8284

The big square has area 4.8284^2 = 23.3137

Small triangles areas to remove add up to sqr(2)^2x4 triangles/2halves = 2x2 =4

Octagon = big - triangles = 19.3137

Next Octagon - midpointsquare Midpoints are half way along the invisible triangles long side length 2. As it’s a right angle triangle it’s pair of equal short sides are sqr(2) Pythagoras again.

As the inner square goes from midpoint of sqr(2) to the side length of the octagon plus another midpoint then the inner square removed has a side of Sqr(2)/2 + 2 + sqr(2)/2 = 1.4142 + 2 = 3.4142

Area is 3.4142^2 = 11.6568

Octagon - square = 19.3137 - 11.6568 Approx. = 7.657 rounded up

Note: there’s an interesting symmetry when you add up the negative shape spaces first and I guess that’s what Arjen mentions in “folding the flaps” :)

Slightly different from Arjen Vreugdenhil but using the same idea of folding in the red areas to create a square of side two units:

The area of the octagon with side of two is 19.3137...

The red portion accounts for half the area of the octagon minus the square: 19.3137 - 4 = 15.3137

Answer: 15.3137 / 2 = 7.657

For area of octagon:

Let $AB = r$ and $AD = h$ .

$BC = 2 \implies BD = 1, \angle{BAD} = \dfrac{\pi}{8} \implies r = \dfrac{1}{\sin(\dfrac{\pi}{8})} \implies h = \cot(\dfrac{\pi}{8}) \implies$ $A_{octagon} = 8 \cot(\dfrac{\pi}{8})$ .

Using $h = \cot(\dfrac{\pi}{8})$ and letting $L$ be the distance between two consecutive vertices of the square $\implies L^2 = 2 \cot^2(\dfrac{\pi}{8})$ = $A_{square} \implies Area_{red} =$ $8 \cot(\dfrac{\pi}{8}) - 2 \cot^2(\dfrac{\pi}{8}) =$ $\boxed{7.656854.}$ .

If you take the 4 red parts and push the top one down, the bottom one up, the left one right and the right one left and let the side length of the big square be denoted as $a$ its easy to see that $a^2 - 2^2 = A(R)$ where $A(R)$ is the area of the red portion.

Since the vertices of the big square intersect the sides of the octagon at its midpoints, we can easily see that:

$a = 2 + 2 * sin(\frac{\pi}{4}) = 2 + \sqrt{2}$

Therefore:

$A(R) = (2 + \sqrt{2})^2 - 4 = 4 + 4\sqrt{2} + 2 - 4 = 4\sqrt{2} + 2 \approx 7.657$

As explained in Zain Majumder 's answer, by dropping a perpendicular from one of the octagon's vertices on the square's side, we create a $45 - 90 - 45$ triangle.

Also note that the hypothenuse $H$ of an isosceles right-angled triangle of side length $l$ is always $H=l\sqrt{2}$ . Therefore, the line segment which is common to the triangle and the square has length $l=\frac{H}{\sqrt{2}}=\frac{\frac{2}{2}}{\sqrt{2}}=\frac{\sqrt{2}}{2}$ . Thus, the side length of the square is $l=2+2\cdot \frac{\sqrt{2}}{2}=2+\sqrt{2}$ . Hence, the area of the square is $l^2=4+4\sqrt{2}+2=6+4\sqrt{2}=2(3+2\sqrt{2})$ .

Also, the formula for the area of an octagon is $2(1+\sqrt{2})l^2$ , so $A_{octagon}=8(1+\sqrt{2})$ .

Subtracting, $8(1+\sqrt{2}) - 2(3+2\sqrt{2}) \approx 7.6568542495$ . So our result is 7.6568542495 .

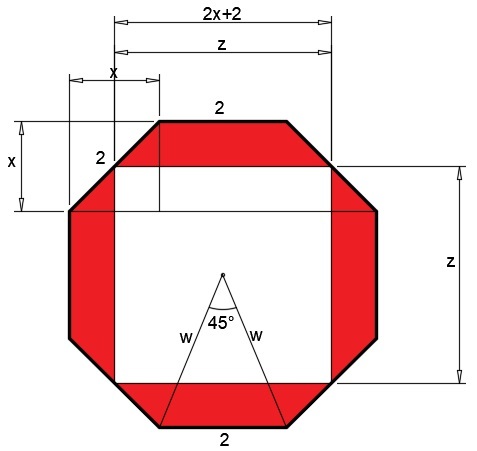
Consider my diagram. By pythagorean theorem, we have

$2^2=x^2+x^2$ $\implies$ $x=\sqrt{2}$

Then,

$z=\dfrac{2x+2+2}{2}=\dfrac{2x+4}{2}=x+2=\sqrt{2}+2$

By cosine rule, we have

$2^2=w^2+w^2-2(w)(w)(\cos 45)$ $\implies$ $w^2 \approx 6.8284$

The area of the red region region is equal to the area of the regular octagon minus the area of the square, we have

$A=8\left(\dfrac{1}{2}\right)(w^2)(\sin 45)-z^2=4(6.8284)(\sin~45)-(\sqrt{2}+2)^2\approx \boxed{7.657}$

Merry x-mas and a happy new year to all. Let's welcome year 2018 with a big bang !!

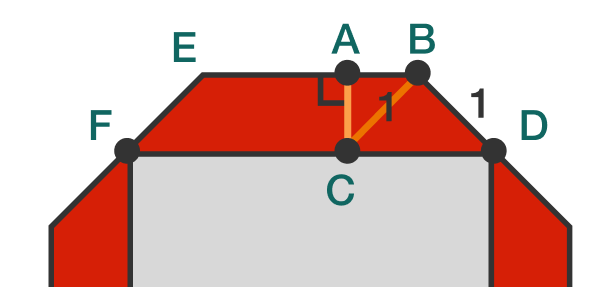
Add a side $BC$ that is congruent to $BD$ as shown and drop a perpendicular from $C$ to the opposite side. We know from the angles of the regular octagon that $BCD$ and $ABC$ are both isosceles right triangles. Therefore side $AC$ measures $\frac{1}{\sqrt{2}} .$

The area of the parallelogram $EBCF$ is the height times the width, that is, $\frac{1}{\sqrt{2}} \times 2 = \frac{2}{\sqrt{2}} = \sqrt{2}.$ The area of the triangle $BCD$ is just half the base times the height, that is, $\frac{1}{2} \times 1 \times 1 = \frac{1}{2}.$ These add together so that one of the four red portions has an area of $\sqrt{2} + \frac{1}{2} ,$ and all four portions together have an area of $4 \left( \sqrt{2} + \frac{1}{2}\right) \approx 7.656854 .$