Embiggen this Circle
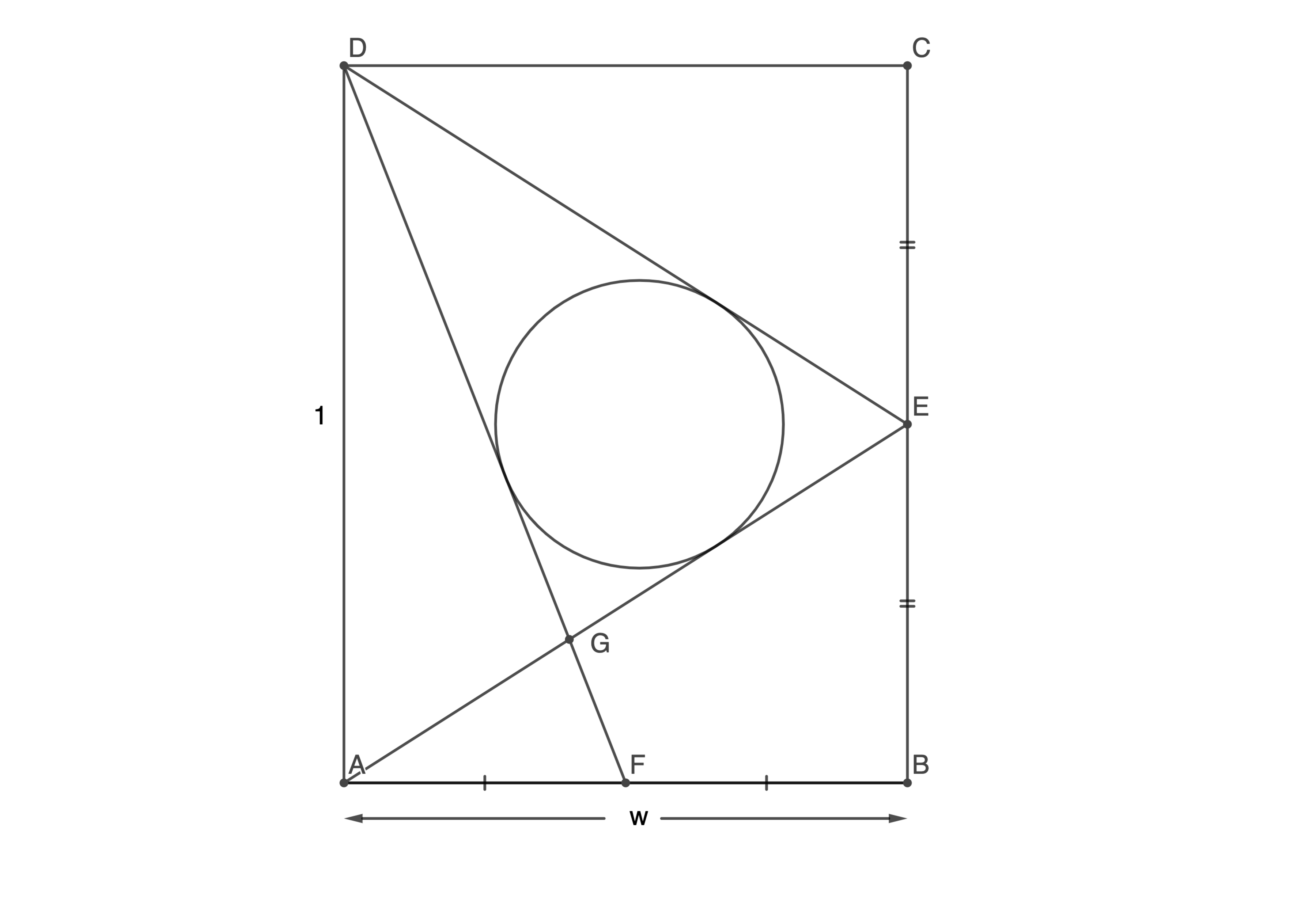
is a rectangle. and . and are the midpoints of and , respectively.
Find the value of which maximizes the ratio of the area of the circle to the area of the rectangle.
If this value can be expressed as , where is square-free and and are positive integers, and submit .
The answer is 506.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let us plot this into a Cartesian plane, with A ( 0 , 0 ) , B ( w , 0 ) , C ( w , 1 ) , D ( 1 , 0 ) , E ( w , 2 1 ) , F ( 2 w , 0 ) .
The coordinate of the G can be found by finding the intersection point between the two straights A E and D F :
{ Straight line A E : Straight line D G : y = 2 1 ⋅ w x = 2 w x w / 2 x + 1 y = 1 ⇒ G = ( 5 2 w , 5 1 )
Let r denote the radius of the circle, then r = s A , where A and s denotes the area and semiperimeter of the triangle D E G , respectively.
A can be computed by finding the complementary area. That is, ( Area of rectangle A B C D ) − A = ( Area of triangle D A F ) + ( Area of triangle A B F ) + ( Area of triangle D C E ) − ( Area of triangle G A F )
In the right-hand-side of the equation above, the first three areas are easy to compute because they are all right-angle triangles. The last area can be computed using shoelace formula .
Simplify all these, we get A = 1 0 3 w ( 1 )
By Pythagorean theorem , we can find all the side lengths of the triangle D E G . Thus, we can obtain s = 2 D E + E G + G D = 5 1 ( 4 + w 2 + 2 1 + 4 w 2 ) ( 2 )
Let P denote the ratio of the area of the circle to the area of the triangle, so P = 1 ⋅ w π r 2 = 4 9 ⋅ ( 4 + w 2 + 2 1 + 4 w 2 ) 2 w
Maximizing P is equivalent to minimizing Q : = w ( 4 + w 2 + 2 1 + 4 w 2 ) 2 = 1 7 w + w 4 w 2 + 4 ⋅ 4 w 2 + 1 + w 8
At its critical point(s), d w d Q = 0 . Apply quotient rule and simplify all the tedious algebra, we get w = 8 4 8 1 − 1 7 .
Obviously Q has no maximum value because we can set w to be unboundedly large, so the critical point above must be a minimum value.
Hence, the ratio in question is maximized when w = 8 4 8 1 − 1 7 . The answer is 4 8 1 + 1 7 + 8 = 5 0 6 .