Emf in the Archimedean spiral
A wire is bent into the shape of an planar Archimedean spiral which in polar coordinates is described by the equation r = b θ . The spiral has N = 1 0 0 turns and outer radius R = 1 0 cm ( R is the distance from point O to point T). Note that in the figure below we show a spiral having only 3 turns. The circuit is placed in a homogeneous magnetic field perpendicular to the plane of the spiral. The time dependence of the magnetic field induction is given by B = B 0 cos ( ω t ) where B 0 = 1 μ T and ω = 2 × 1 0 6 s − 1 . Determine, the amplitude of the emf in Volts induced in the circuit.
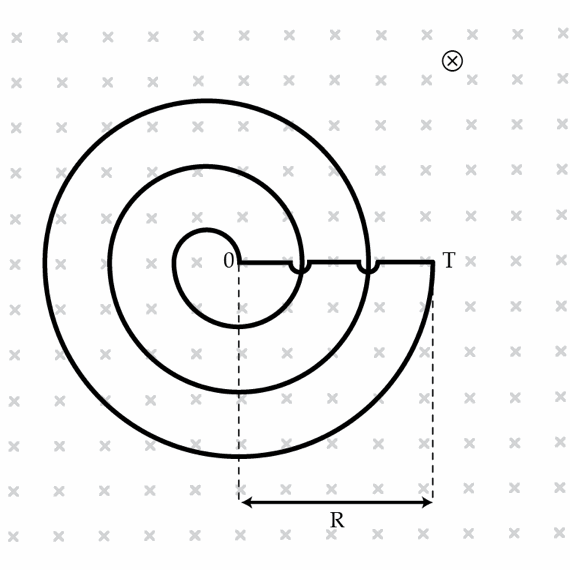
The answer is 2.094.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
9 solutions
Moderator note:
Very nice use of an N large approximation!
Firstly, let's calculate the region's area A :
In polar coordinates: A = ∫ 2 r 2 d θ = ∫ 0 1 0 0 ∗ 2 π 2 b 2 θ 2 d θ = 6 b 2 ( 2 0 0 π ) 3 and since that r = 1 0 c m when θ = 2 0 0 π , then b = 2 0 0 π 0 . 1
So, the area is A = 6 ( 0 . 1 ) 2 ∗ 2 0 0 π = 1 . 0 4 7 1 9 7 5 5 1 2 m 2
Now, let's calculate the magnetic flux: ϕ = B ( t ) A
Using the Faraday's Law, we have the emf induced : ϵ = d t d ϕ
So, ϵ = − B o ω A s i n ( ω t ) . Therefore, the amplitude of the emf in Volts induced is ϵ m a x = B o ω A = 1 ∗ 1 0 − 6 ∗ 2 ∗ 1 0 6 ∗ 1 . 0 4 7 1 9 7 5 5 1 2 = 2 . 0 9 4 V
The induced emf by changing magnetic field is given by
ε = − N d t d ( Φ ) where Φ = B A ⊥ .
The area of the spiral is one-third of the circle enclosing it so that
A ⊥ = 3 π r 2 = 3 π ( 0 . 1 m ) 2 = 3 0 0 π m 2 .
Solving for ε ,
ε = − N d t d ( Φ ) = − N d t d ( B A ⊥ ) = − N B 0 A ⊥ d t d ( cos ( ω t ) )
ε = N B 0 A ⊥ ω sin ( ω t ) .
Substituting the given values, the amplitude of the induced emf is
ε m = ( 1 0 0 ) ( 1 × 1 0 − 6 μ T ) ( 3 0 0 π m 2 ) ( 2 × 1 0 6 s − 1 ) = 2 . 0 9 4 v o l t s .
My apologies. At the last part, it's supposed to be 1 × 1 0 − 6 T , not 1 × 1 0 − 6 μ T
From Faraday's Law, we have $$\mathcal{E}=-\frac{d\Phi}{dt}=-\frac{d}{dt}\left[BA\right].$$ We are given $$B=B 0 \cos{\left(\omega t\right)},$$ and we can calculate the total are inside the circuit by evaluating a polar integral of r = 2 π N R θ , which is the general form for an Archimedean spiral with outer radius R and N turns. $$A=\frac{1}{2}\int {0}^{2\pi N}\left({\frac{R}{2\pi N}\theta}\right)^2 \ d\theta=\frac{\pi}{3} N R^2$$ Substituting back into Faraday's Law gives $$\mathcal{E}=-\frac{d}{dt}\left[\frac{\pi}{3} N R^2 B_0 \cos{\left({\omega t}\right)}\right]$$
$$=\frac{\pi}{3} N R^2 B_0 \omega \sin{\left({\omega t}\right)}.$$
The amplitude a of this function is just the coefficient of the sine function.
$$a=\frac{\pi}{3} N R^2 B_0 \omega $$ $$=\frac{\pi}{3} \left(100\right) \left(0.10 \ \mathrm{m}\right)^2 \left(1 \times 10^{-6} \ \mathrm{T}\right) \left(2 \times 10^6 \mathrm{s^{-1}}\right) $$ $$= \frac{2\pi}{3} \ \mathrm{V} \approx \fbox{2.094 V}. $$
First we determine the b in the equation r = b θ . We note that because there is 100 spirals, that means that θ = 1 0 0 ( 2 π ) when r = 0 . 1 m . Thus we get the equation as r = 2 0 0 0 π 1 θ . The flux through the surface is given as \Phi_B = \iint\limits_A \bf{B}\, \dot\, \bf{dA} \ \ . We know that the magnetic field is parallel to the normal of the surface, and that B has no dependence on the area, so we can write the equation as Φ B = B A ∬ d A Doing the integral in polar coordinates, we have Φ B = B ∫ 0 2 0 0 π ∫ 0 b θ r d r d θ . Solving this, we end up with Φ B = 3 π B . Now to find the amplitude of the emf, we use Faraday's law of induction, E = − d t d Φ B . Since B = B 0 c o s ω t , we obtain E = 3 π B 0 ω s i n ω t . The amplitude of the emf would thus be 3 π B 0 ω = 2 . 0 9 V .
Let's find b . If N = 1 0 0 we'll have θ = 2 π ⋅ 1 0 0 . So: $$ r = b\theta \Rightarrow R = b\cdot 200\pi \Rightarrow b = \frac{1}{20\pi} $$ Calculating ϵ : $$ \phi = B\cdot A \Rightarrow \epsilon = -\frac{d\phi}{dt} = - A\cdot\frac{dB}{dt} $$ $$ \epsilon = AB 0\omega\sin(\omega t) $$ So, we observe that the amplitude of emf is A B 0 ω . Here we need to calculate the area of the spiral: $$ A = \int\int rdrd\theta = \int {\theta = 0}^{200\pi}\frac{r^2}{2}d\theta = \int {\theta = 0}^{200\pi}\frac{b^2\theta^2}{2}d\theta = \frac{b^2(200\pi)^3}{6} $$ Finally, applying the corresponding values: $$ \epsilon {max} = AB_0\omega = 2.094 $$
By Faraday's Law of Electromagnetic Induction, ε = − N d t d Φ B . Since Φ B = B A and the area enclosed by an Archimedean spiral is 3 1 the area of the circle enclosing it, we have that ε = − N d t d ( B 0 c o s ( ω t ) 3 1 π r 2 ) . Therefore, we have that ε = N B 0 3 1 π r 2 ω s i n ( ω t ) , so the amplitude of the induced emf is N B 0 3 1 π r 2 ω . Substituting in our given values, we get that our answer is 1 0 0 ( 1 0 − 6 ) ( 3 1 ) ( π ) ( 0 . 1 ) 2 ( 2 ∗ 1 0 6 ) ≈ 2 . 0 9 4
According to Maxwell's equations, we can calculate the EMF as E = d t d ∮ B d S . As the induction of the magnetic field is constant over space (i.e. ∇ B = 0 ), we can take it outside of the integral. Also note, that since the spiral is flat, d S is always parallel to B , allowing us to substitute B d S for B d S .
The area enclosed by the spiral can be calculated as S = 2 1 ∫ 0 2 π × 9 9 . 7 5 b 2 ϑ 2 d ϑ = 2 b 2 3 ( 2 π × 9 9 . 7 5 ) 3 , where we took into account that actually (according to the figure) the spiral makes a quarter of a turn less than stated.
b can be calculated from the equation for a spiral, substituting r = 0 . 1 m and ϑ = 2 π × 9 9 . 7 5 . So, b = 1 9 9 5 π 1 . Combining everything we have got thus far, E a m p = B 0 S ω = 1 0 − 6 × 4 0 0 1 3 3 π × 2 × 1 0 6 = 2 . 0 8 9 ( V ) .
The Maxwell-Faraday relationship governs the behavior of yet another closed wire in a field!
− d t d ϕ B = E
Instead of a simple circle or square, we have the spiral of Archimedes which has a series of overlapping elements, each subsequent turn of the spiral containing the area of the turn which precedes it. The field is uniform, so the flux is given by
ϕ B = A e f f B ⋅ k ^
where A e f f is the effective area of the entire spiral.
We can calculate the total effective area by integrating the radius around the N turns. This is given by
A e f f = 0 ∫ b θ 0 ∫ 2 0 0 π r d r d θ = 3 4 b 2 N 3 π 3
We know that r = b θ and we also know that the radius at 100 turns ( θ = 2 0 0 π ) is 0.1 cm , thus b = 2 0 0 0 π 1 .
Plugging this all in, we find A e f f = 3 π .
Therefore, ϕ B = 3 π B 0 cos ω t making the magnitude of d t d ϕ B equal to 3 π B 0 ω = 3 2 π ≈ 2 . 0 9 4 .
Because the number of turns is big, we suppose each turn is nearly a circle.
The emf induced in the circuit is: E = − d t d Φ = − d t d B Σ S , where Σ S is the total area of all circles.
Because the number of circles is big, we can calculate Σ S by calculate the average area of all circles: S a v e r a g e = 0 ∫ R R π r 2 d r = 3 π R 2 .
Therefore, Σ S = N S a v e r a g e = 3 N π R 2 .
So E = ω B 0 sin ( ω t ) 3 N π R 2 .
The amplitude of E is 3 1 π R 2 N ω B 0 = 2 . 0 9 4 V .