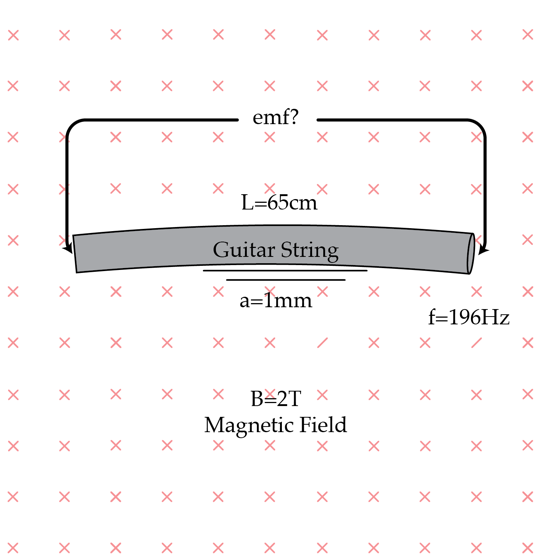
Emf on the G string

We know that the induced $\mathrm{emf}$ in a conductor moving in a magnetic field is calculated by $\mathrm{emf}=LBv$ , where L is the length of the conductor in the magnetic field, but since the string’s vertical speed $v(t,x)$ is not the same everywhere along its lenght, this formula becomes

$\mathrm{emf}=B \int\limits_0^L \ v(t,x) \mathrm{d}x$ To obtain the velocity $v(t,x)$ , we take the derivative of $y(t,x)$ with respect to $t$ .

$v(t,x)=\frac{\partial y(t,x)} {\partial t}=-2\pi af\sin(2 \pi ft) \sin(\frac {\pi x}{L})$

Substituting this into the integral for $\mathrm{emf}$ yields:

$\mathrm{emf}=B \int\limits_0^L \ (-2\pi af\sin(2 \pi ft) \sin(\frac {\pi x}{L})) \mathrm{d}x=$

$=-2\pi B af \sin(2 \pi ft) \int\limits_0^L \ \sin(\frac {\pi x}{L}) \mathrm{d}x =$

$=-2\pi B af\sin(2 \pi ft) [-\frac{L}{\pi} \cos(\frac {\pi x}{L})]_0^L=-4LafB\sin(2 \pi ft)$

We see that this is the formula for an alternating voltage, and we want to find the peak value. And since $-1\leq sin(\theta)\leq 1, \forall \theta \in \mathbb{R}$ , we can see that the expression above is maximal when $\sin(2 \pi ft)=-1$ (or $+1$ , the sign doesn’t really matter, it only shows in which direction the current is flowing), which gives:

$\mathrm{emf}_{max}=4LafB$

Plugging in numbers (in SI units) gives:

$\mathrm{emf}=4\times 0.65\times 0.001\times196\times2=1.02 \mathrm{V}$

Faraday's Law of Induction states:

$\varepsilon = - \frac {d \Phi_B } {d t}$ .

where $\Phi_B = B \cdot A$ for a B-field perpendicular to the area plane.

Therefore, $\varepsilon = - \frac {d \Phi_B } {d t} = -\frac {d} {d t} (B \cdot A) = -B \frac {d A} {dt}$ , since B is constant.

In this problem, the instantaneous flux area is determined by the vibrating string, where $A = \int_{0}^{L} y \cdot d x + C$ , where C is an unknown constant.

Accordingly, $\varepsilon = -B \frac {d A} {dt} = -\frac {d} {dt} [\int_{0}^{L} y \cdot d x]$ .

Given $y(t,x)=a \cos(2πft) \sin(\frac {\pi x} {L})$ , $\int_{0}^{L} a \cos(2πft) \sin(\frac {\pi x} {L}) \cdot d x = - \frac {a L} {\pi} \cos(2πft) \cos(\frac {\pi x} {L}) |_{0}^{L} = - \frac { 2 a L} {\pi} \cos(2πft)$ .

Therefore, $\frac {d A} {d t} = 4 f a L \sin(2πft)$ .

Finally, $\varepsilon = -B \frac {d A} {dt} = - 4 B f a L \sin(2 \pi ft)$ .

At maximum amplitude, $|- \sin(2\pi f t)|=1$ . Therefore $\varepsilon_{max} = 4 B f a L = 4 (2 T)(196 s^{-1})(0.001 m)(0.65 m) = 1.0192 V$ .

The magnitude of the emf can be found from Faraday's Law $\mathcal{E}=-\frac{d \Phi}{dt}= - B \frac{dA}{dt}$ where A is the area swept out by the string. For a given time t, the area under the curve $y(t,x)= a \cos(2 \pi f t) \sin(\frac{\pi x}{L})$ is simply $A(t)= \int_{0}^{L} y(t,x) dx = \frac{2 a L}{\pi} \cos(2 \pi f t).$ Therefore the emf is given by $\mathcal{E}= 4 a LB f \sin(2 \pi f t) \rightarrow \mathcal{E}_{peak}=1 V.$