Enclosed octagon

This is best approached using coordinate geometry. Let $A = (0, 0)$ , $B= (0, 1)$ , $C= (1, 1)$ and $D= (1,0)$ . Then, we have the equations $AF : y = 2x$ and $BH: y = -2x + 1$ which give the intersection point $\left(\frac {1}{4}, \frac {1}{2}\right)$ . The equations $ED: y = -\frac {1}{2} x+ \frac {1}{2}$ and $BH: y = -2x + 1$ gives the intersection point $\left( \frac {1}{3}, \frac {1}{3} \right)$ . Hence, the side length of the octagon is

$s = \sqrt{ \left( \frac {1}{4} - \frac {1}{3} \right)^2 + \left( \frac {1}{2} - \frac {1}{3} \right)^2} = \sqrt{ \frac {5}{144} }$

Thus $s^2 = \frac {5}{144}$ . Hence $a+b = 149$ .

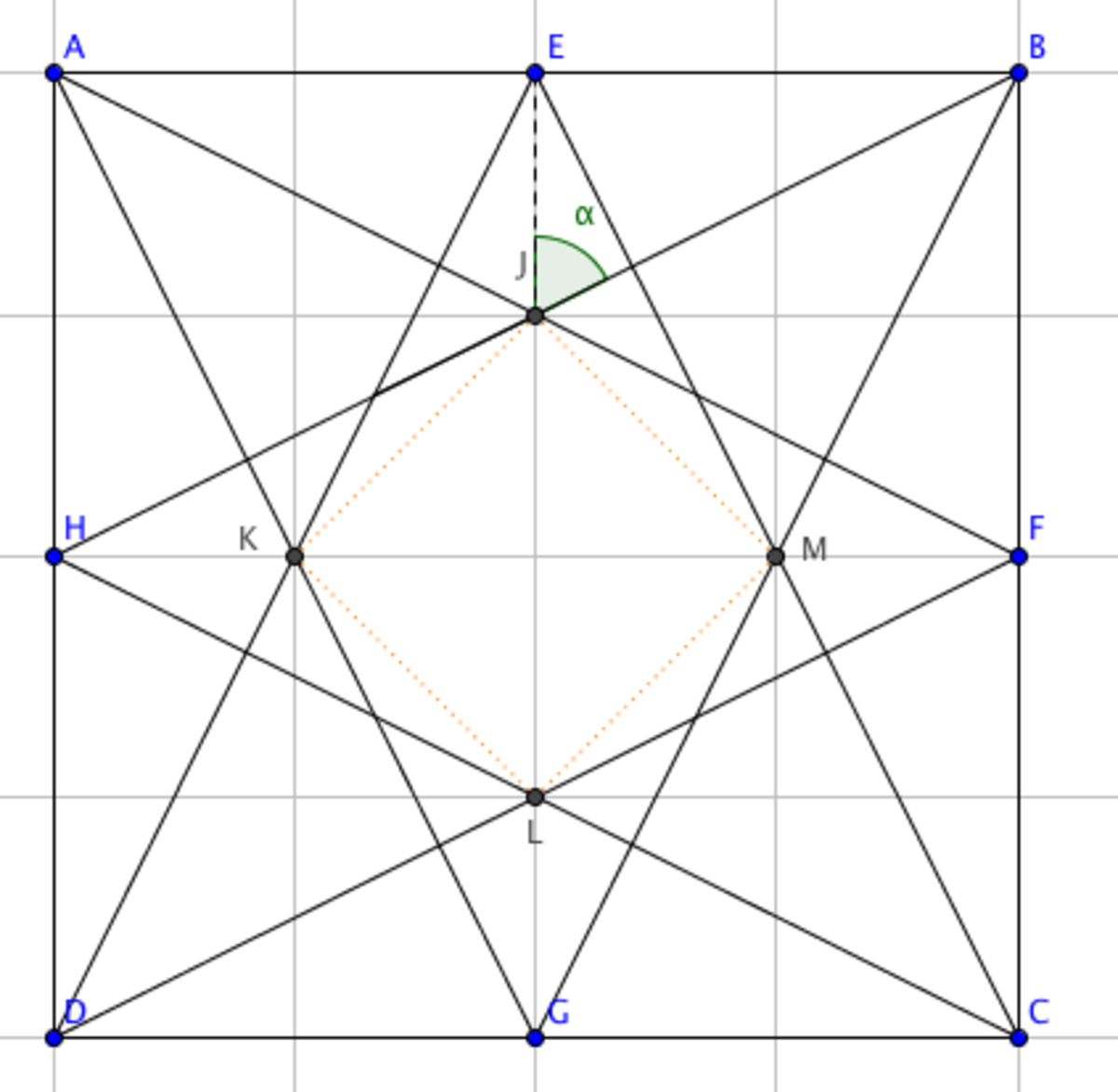
Let all points be labelled as on the diagram above. The grid is 0.25 x 0.25 units. Note that J, K, L, M are on this grid as they are intersection points of diagonals of rectangles (each rectangle being half of the square ABCD). Hence $JK = \frac{1}{4}\sqrt{2}$ .

Note that $\cos \alpha = \frac{EJ}{BJ} = \frac{1}{\sqrt{5}}$ and $\sin \alpha = \frac{BE}{BJ} = \frac{2}{\sqrt{5}}$ .

Now, $\angle HJL = \alpha$ , so $\angle HJK = \alpha - 45$ .

Denoting the intersection of BH and ED by Q, and looking at half of the isosceles triangle JQK, we have:

$JQ = \frac{JK}{2} \div \cos(\angle HJK) =$

$\frac{\sqrt{2}}{8} \div (\cos \alpha \cos 45 + \sin \alpha \sin 45) =$

$\frac{\sqrt{2}}{8} \div (\frac{\sqrt{2}}{2} (\cos \alpha + \sin \alpha) ) =$

$\frac{1}{4(\frac{1}{\sqrt{5}} + \frac{2}{\sqrt{5}})} = \frac{\sqrt{5}}{12}.$