Ending Ellipses
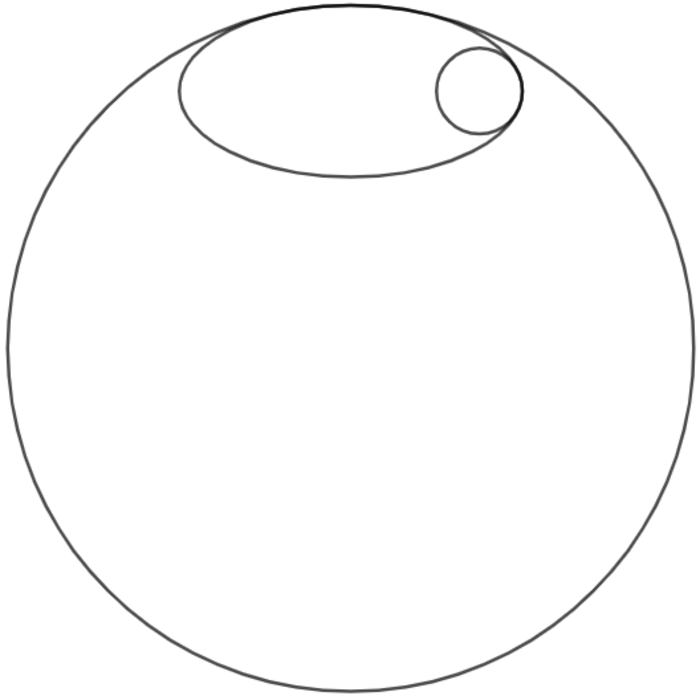
The ellipse whose major and minor axes are respectively and is symmetrically positioned, where its minor axis touches the large circle at one point. In addition, the small circle inscribed in the ellipse also touches at one point. If the ratio of the minimum possible large circle radius to maximum possible small circle radius can be expressed as , where and are coprime positive integers, input as your answer.
The answer is 65.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If you place the ellipse so that its center is at the origin, its equation is 2 4 2 x 2 + 6 2 y 2 = 1 , which rearranges to x 2 + 1 6 y 2 = 5 7 6 .
The large circle with a radius of R will have a center of ( 0 , 6 − R ) , so it has an equation of x 2 + ( y − 6 + R ) 2 = R 2 .
Substituting x 2 = 5 7 6 − 1 6 y 2 , the equation becomes 5 7 6 − 1 6 y 2 + ( y − 6 + R ) 2 = R 2 and rearranges to ( y − 6 ) ( y − 1 5 2 ( R − 2 1 ) ) = 0 , which means that the ellipse and the circle intersect at y = 6 and y = 1 5 2 ( R − 2 1 ) .
For the ellipse to be inscribed and not intersect the circle, 1 5 2 ( R − 2 1 ) = y ≥ 6 , which solves to R ≥ 9 6 .
The small circle with a radius of r will have a center of ( 2 4 − r , 0 ) , so it has an equation of ( x − 2 4 + r ) 2 + y 2 = r 2 .
Substituting y 2 = 1 6 1 ( 5 7 6 − x 2 ) , the equation becomes ( x − 2 4 + r ) 2 + 1 6 1 ( 5 7 6 − x 2 ) = r 2 and rearranges to ( x − 2 4 ) ( y − 1 5 8 ( 5 1 − 4 r ) ) = 0 , which means that the ellipse and the circle intersect at x = 2 4 and x = 1 5 8 ( 5 1 − 4 r ) .
For the ellipse to be inscribed and not intersect the circle, 1 5 8 ( 5 1 − 4 r ) = x ≥ 2 4 , which solves to r ≤ 2 3 .
Therefore, the ratio of the minimum possible large circle radius to maximum possible small circle radius is 2 3 9 6 = 1 6 4 , so a = 6 4 , b = 1 , and a + b = 6 5 .