Endless Circles and Triangles
An equilateral triangle is drawn inside a
circle
of
radius
1, such that all vertices of the triangle touch the circle.
Another circle is drawn inside the triangle such that the new circle touches each side of the triangle once.
Another equilateral triangle is drawn inside the second circle as described above, and a third circle is drawn inside the second triangle as described above.
This process is continued to form an infinite number of circles and triangles.
The first three circles and triangles are shown in the picture below.
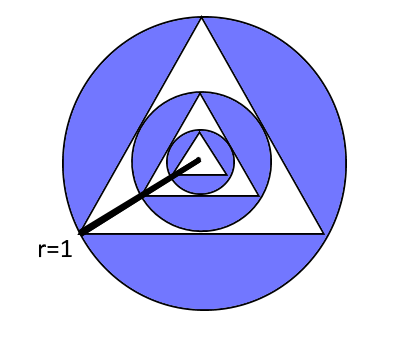
What is the ratio (in percentage) of the area of the blue region to the area of the largest circle?
Give your answer to 1 decimal place. (For example, if the answer is 84.5%, write 84.5.)
The answer is 78.2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Length and Area Problem Solving
Let the radius of the largest circle be r 1 = 1 . Let the side length of the first triangle be a 1 . Then, let the area between the n:th and the (n+1):th circle be A n . The radius of the n:th circle is r n and the side length of the n:th triangle is a n .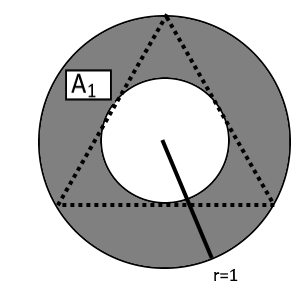
A 1 = ( π r 1 2 − π r 2 2 )
The first triangle can be divided in three triangles congruent to each other, with two sides being 1 unit long and their angle 120 degrees. The area of one triangle is 2 1 × 1 × 1 × sin 1 2 0 = 4 3 .
This means the area of the whole triangle is B 1 = 3 × 4 3 .
That area is also 2 1 a 1 2 sin 6 0 = 4 3 a 1 2 . We get an equation:
4 3 a 1 2 = 3 × 4 3
a 1 2 = 3
a 1 = 3 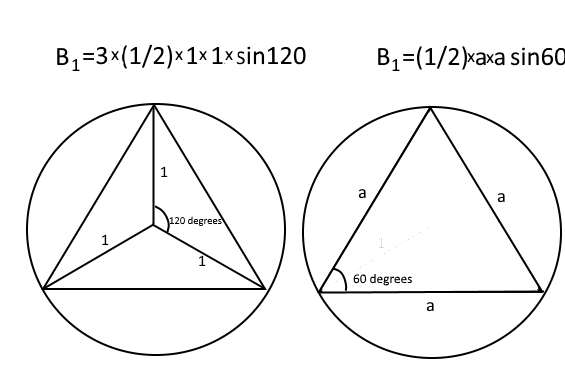
Next we will find out the value of r 2 . We can separate a quadrilateral from the triangle. This quadrilateral has two straight angles, two sides with length r 2 and two sides with length 2 a 1 . This quadrilateral can be cut in two halves, triangles with a straight angle, a 30 degrees angle and a 60 degrees angle. The side towards the 60 degrees angle is 2 a 1 units long and the one towards the 30 degrees angle is r 2 units long. We get an equation:
tan 3 0 = ( 2 3 ) r 2
r 2 = 2 3 × 3 1
r 2 = 2 1
So A 1 = π − π × ( 2 1 ) 2 = 4 3 π 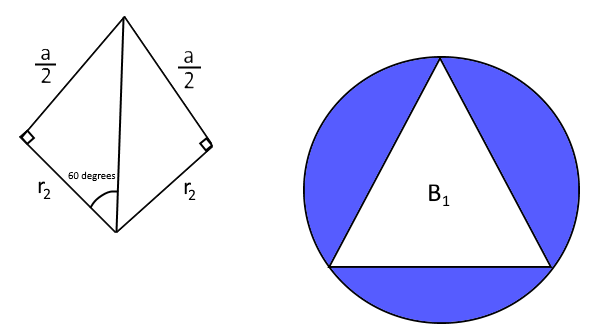
Let the area of the coloured regions between the n:th and the (n+1):th circle be C n . In this case
C 1 = π × 1 2 − B 1 = π − 4 3 3
Let A = A 1 + A 2 + A 3 + . . . be the whole area of the largest circle, while C = C 1 + C 2 + C 3 + . . . is the area of all coloured regions. Due to similarity of the regions between circles,
A 1 C 1 = A 2 C 2 = A 3 C 3 = . . . = k , where k is constant. We get a result
A C = A 1 + A 2 + A 3 + . . . C 1 + C 2 + C 3 + . . . = A 1 + A 2 + A 3 + . . . k A 1 + k A 2 + k A 3 + . . . = k
A C = A 1 C 1
This means, we get the percentage of coloured regions inside the largest circle by calculating
A 1 C 1 = 4 3 π π − 4 3 3 = 0 . 7 8 2 0 0 4 . . .
so the approximate percentage with the accuracy of one decimal is 7 8 . 2 %.