Endothermic To Exothermic

Classical Mechanics Level 5

Source : Resonance AIOT Source : Resonance AIOT

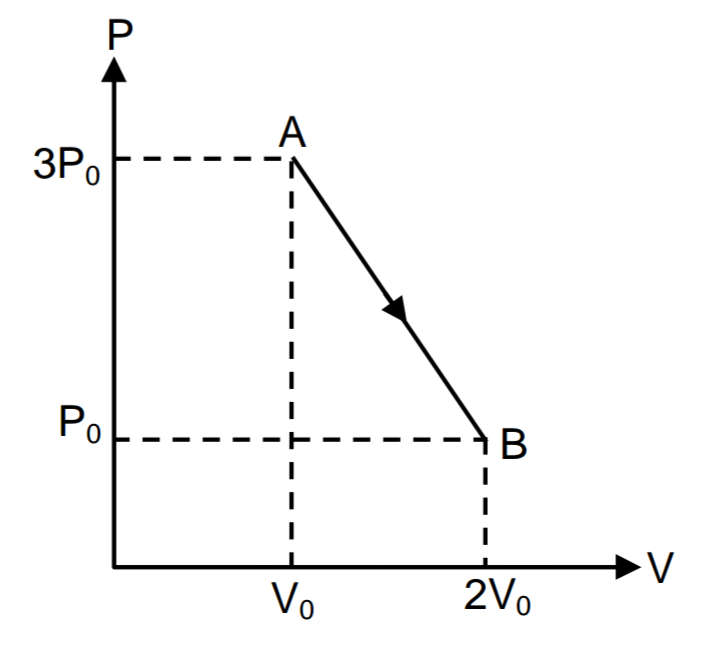
An ideal diatomic gas undergoes process A B AB for which P V PV indicator diagram is shown. At some time during this process, it changes from being endothermic to being exothermic. At that time, the volume of the gas is 5 λ V 0 72 \dfrac{5\lambda V_{0}}{72} . Find λ \lambda .


The answer is 21.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Equation of the straight line AB is :

P = 5 P 0 − 2 P 0 V V 0 P=5P_{0} - \dfrac{2P_{0}V}{V_{0}}

Q Q (Heat) as a function of volume is :

Q = 35 P 0 V 2 − 6 P 0 V 2 V 0 − 23 P 0 V 0 2 Q=\dfrac{35P_{0}V}{2}-\dfrac{6P_{0} V^2}{V_{0}}-\dfrac{23P_{0}V_{0}}{2}

Above equation is a downward parabola with apex occuring at V ′ = 35 V 0 24 V'=\dfrac{35V_{0}}{24} . After V ′ V' , Q Q is decreasing (Heat must have started evolving after the apex leading to a fall in curve)

Hence V ′ V' must be the required volume .

V ′ = 35 V 0 24 \boxed{V'=\dfrac{35V_{0}}{24}}

2 Helpful 0 Interesting 1 Brilliant 0 Confused

We look for a point on A B AB that is tangent to the adiabatic curve P V γ = k PV^\gamma = k , or P = k V − γ P = kV^{-\gamma} , with γ = 7 / 5 \gamma = 7/5 . The derivative is d P / d V = − γ k V − γ − 1 = − γ P / V dP/dV = -\gamma kV^{-\gamma-1} = -\gamma P/V . This derivative must match the slope of A B AB , which is − 2 P 0 / V 0 -2P_0/V_0 .

Thus d P d V = − 7 5 P V = − 2 P 0 V 0 , \frac{dP}{dV} = -\frac 7 5 \frac{P}{V} = -2\frac{P_0}{V_0}, so that 7 P P 0 − 10 V V 0 = 0 ; 7\frac{P}{P_0} - 10\frac{V}{V_0} = 0; but we also have for line A B AB P P 0 + 2 V V 0 = 5. \frac{P}{P_0} + 2\frac{V}{V_0} = 5. Multiply the last equation by 7 and subtract the first to find 24 V V 0 = 35 , 24\frac{V}{V_0} = 35, so that V = 35 V 0 24 = 5 ⋅ 7 ⋅ 3 ⋅ V 0 24 ⋅ 3 . V = \frac{35V_0}{24} = \frac{5\cdot \boxed{7\cdot 3}\cdot V_0}{24\cdot 3}. Thus the answer is 21 \boxed{21} .

Arjen Vreugdenhil - 3 years, 3 months ago

Log in to reply

Thanks , I commited a silly mistake while solving :)

A Former Brilliant Member - 3 years, 3 months ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...