Endpoint 2020
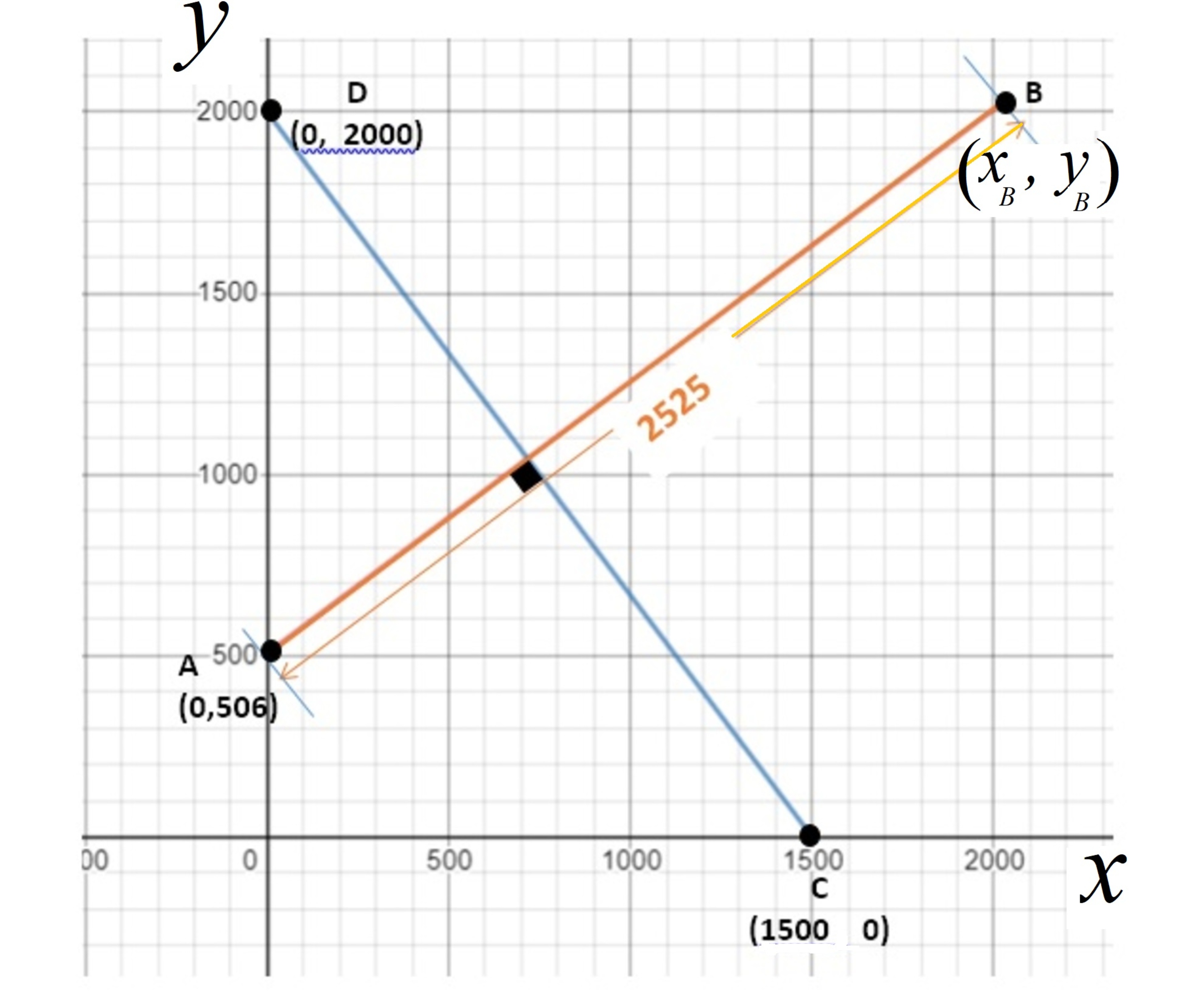
The line segment A B is 2 5 2 5 long and the line segment D C is perpendicular to A B . If the coordinates of the endpoint B are ( x B , y B ) , find ( x B − y B ) .
The answer is -1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
@Ossama Ismail , please use the standard lowercase x and y and not the uppercase for axis and coordinates. Put line segments A B and D C and number 2 5 2 5 in LaTex.
Happy New Year
Wishing you a Happy New Year with the hope that you will have many blessings in the year to come. Thanks for your brilliant solutions. I am always enjoying your solutions to my problems.
The line C D can be modeled as y = − 3 4 x + 2 0 0 0 and A B as y = 4 3 x + 5 0 6 . If ∣ A B ∣ = 2 5 2 5 , then we can compute x B via the Distance Formula:
( x B − 0 ) 2 + ( y B − 5 0 6 ) 2 = ( x B − 0 ) 2 + ( 4 3 x B + 5 0 6 − 5 0 6 ) 2 = 2 5 2 5 ;
or x B 2 + 1 6 9 x B 2 = 2 5 2 5 ;
or 1 6 2 5 x B 2 = 2 5 2 5 ;
or 4 5 x B = 2 5 2 5 ;
or x B = 2 0 2 0 ⇒ y B = 4 3 ( 2 0 2 0 ) + 5 0 6 = 2 0 2 1 .
Hence, x B − y B = 2 0 2 0 − 2 0 2 1 = − 1 .
We can just solve it using similar triangles see my solution.
Log in to reply
Will do, Chew-Seong.....Happy 2021 and to more ingenious Brilliant solutions!!!
A B ⊥ C D ⇒ A B ⋅ C D = 0 ⇒ ( x − 0 y − 5 0 6 ) ⋅ ( 0 − 1 5 0 0 2 0 0 0 − 0 ) = 0 ⇒ − 1 5 0 0 x + 2 0 0 0 ( y − 5 0 6 ) = 0 ⇒ y − 5 0 6 = 4 3 x ( 1 )
∣ ∣ ∣ A B ∣ ∣ ∣ = 2 5 2 5 ⇒ x 2 + ( y − 5 0 6 ) 2 = 2 5 2 5 ⇒ ( 1 ) x 2 + ( 4 3 x ) 2 = 2 5 2 5 2 ⇒ x > 0 x = 2 0 2 0 ( 2 )
( 1 ) , ( 2 ) ⇒ x − y = x − 4 3 x − 5 0 6 = 4 x − 5 0 6 = 4 2 0 2 0 − 5 0 6 = − 1
Let the orange line be y = 4 3 x + 5 0 6 , the slope = 4 3 as it is perpendicular to blue line with slope = 3 − 4
x B 2 + ( y B − 5 0 6 ) 2 = 2 5 2 5 2 ⟹ x B 2 + ( 4 3 x ) 2 = 2 5 2 5 2 ⟹ x B 2 + 1 6 9 x B 2 = 2 5 2 5 2 ⟹ 2 5 x B 2 = 1 6 × 2 5 2 5 2 ⟹ 5 x B = 4 × 2 5 2 5 ⟹ x B = 4 × 5 0 5 = 2 0 2 0 ⟹ x B − y B = 4 1 x B − 5 0 6 = 5 0 5 − 5 0 6 = − 1
Of course, y B = 2 0 2 1 , Happy New Year!
Answer
= (4/5)(2525) - [(3/5)(2525) + 506]
= 2020 - 2021
= -1
Let O be the origin ( 0 , 0 ) ; and A E and B E be parallel to the x - and y -axis respectively. Then we note that △ A B E and △ C D O are similar and △ C D O is a 3 - 4 - 5 right triangle. Since A B = 2 5 2 5 , x B = A E = 5 4 × 2 5 2 5 = 2 0 2 0 and y B = B E + 5 0 6 = 5 3 × 2 5 2 5 + 5 0 6 = 2 0 2 1 ( Happy New Year ) and x B − y B = − 1 .