Energy Accounting (3-22-2020)

Electricity and Magnetism Level 3

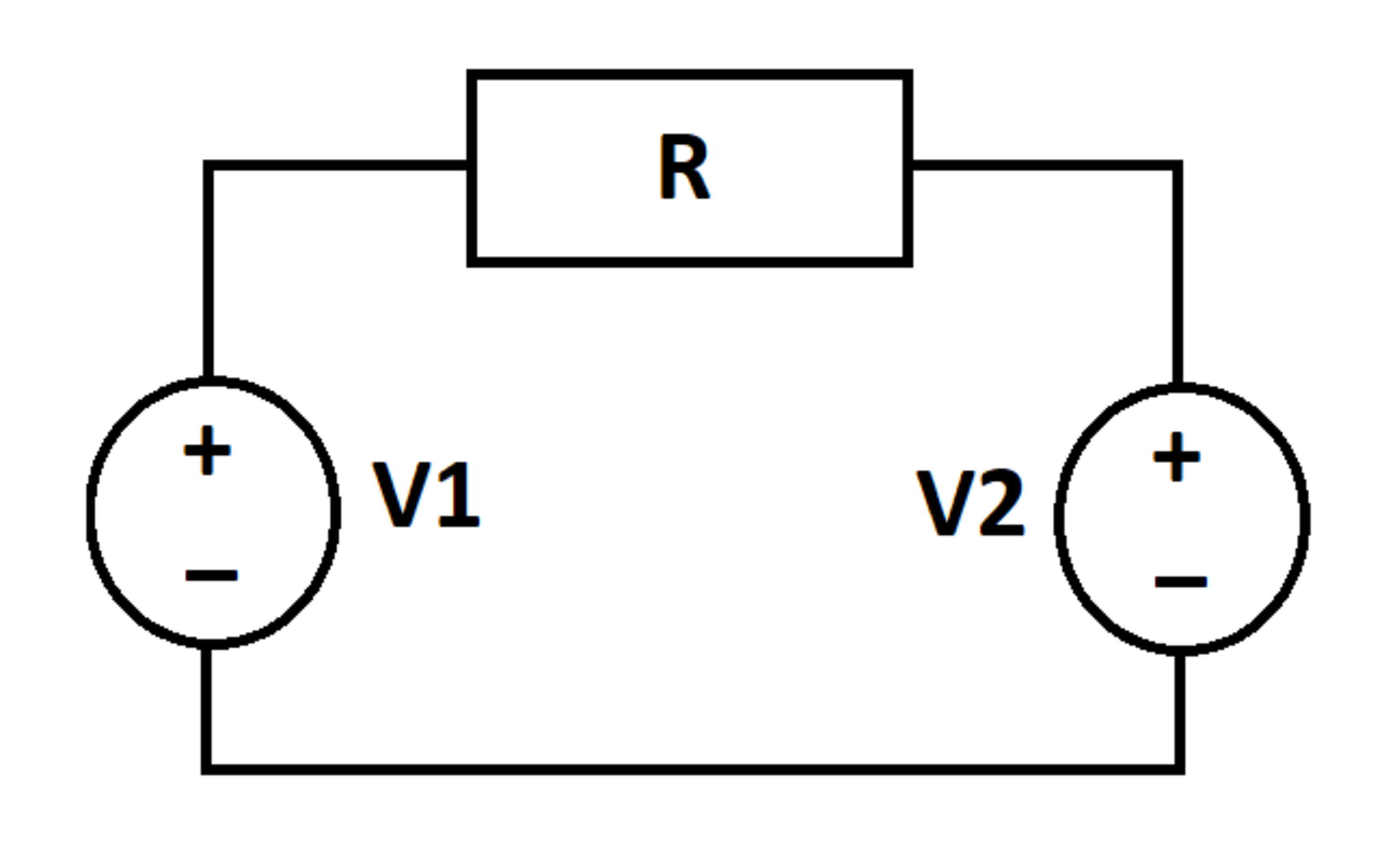
Two AC voltage sources are connected across a resistor as shown. Let E 1 ( t ) E_1(t) be the cumulative energy supplied (outputted) by V 1 V_1 from time t = 0 t = 0 to time t t . E 2 ( t ) E_2(t) is the same, but for V 2 V_2 . Let E R ( t ) E_R(t) be the cumulative energy dissipated in the resistor from time t = 0 t = 0 to time t t .

Determine the value of the following quantity at time t = 1 t = 1 :

Q = E 1 E 2 ( E 1 + E 2 E R ) Q = \frac{E_1}{E_2 } \Big( \frac{E_1 + E_2 }{E_R } \Big)

Details and Assumptions:
1) V 1 ( t ) = sin ⁡ ( 2 t ) V_1(t) = \sin(2 t)
2) V 2 ( t ) = sin ⁡ ( t ) V_2(t) = \sin(t)
3) R = 1 R = 1
4) Be mindful of signs (positive and negative)


The answer is -1.585.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

After some circuit analysis work, we get

E 1 ( t ) = 1 2 R ( t − 1 4 sin ⁡ 4 t − sin ⁡ t + 1 3 sin ⁡ 3 t ) ⟹ E 1 ( 1 ) ≈ 0.1973848208529 E_1(t)=\dfrac{1}{2R}\left (t-\dfrac{1}{4}\sin 4t-\sin t+\dfrac{1}{3}\sin 3t\right )\implies E_1(1)\approx 0.1973848208529

E 2 ( t ) = 1 2 R ( t − sin ⁡ t + 1 3 sin ⁡ 3 t − 1 2 sin ⁡ 2 t ) ⟹ E 2 ( 1 ) ≈ − 0.124539847767 E_2(t)=\dfrac{1}{2R}\left (t-\sin t+\dfrac{1}{3}\sin 3t-\dfrac{1}{2}\sin 2t\right )\implies E_2(1)\approx -0.124539847767

E R ( t ) = 1 2 R ( 2 t − 1 4 sin ⁡ 4 t − 2 sin ⁡ t + 2 3 sin ⁡ 3 t − 1 2 sin ⁡ 2 t ) ⟹ E R ( 1 ) ≈ 0.0728449730858 E_R(t)=\dfrac{1}{2R}\left (2t-\dfrac {1}{4}\sin 4t-2\sin t+\dfrac {2}{3}\sin 3t-\dfrac {1}{2}\sin 2t\right )\implies E_R(1)\approx 0.0728449730858 .

Therefore the given ratio is ≈ − 1.5849 \approx \boxed {-1.5849} .

2 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...