Energy distribution
Nine particles are distributed on three energy levels with the energies E i = i ⋅ E , i = 1 , 2 , 3 so that we have total energy of U = n 1 E 1 + n 2 E 2 + n 3 E 3 = ( n 1 + 2 n 2 + 3 n 3 ) E = 1 6 E with the occupation numbers n i of the state i . These particle numbers meet the requirement N = n 1 + n 2 + n 3 = 9 For which choice of occupation numbers ( n 1 , n 2 , n 3 ) becomes the number of arrangement possibilities (microstates) maximal?
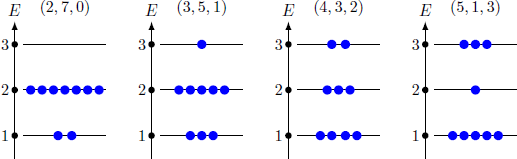
Bonus question: Calculate the particle numbers for the Boltzmann distribution n i ∝ exp ( − E i / k T ) with a temperature k T = 3 E . Which answer option comes next to the Boltzmann distribution?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Great problem! You have a typo in the solution.
The number of permutations for a given choice of occupation numbers is Z ( n 1 , n 2 , n 3 ) = n 1 ! ⋅ n 2 ! ⋅ n 3 ! N ! Therefore, the numbers of microstates are Z ( 2 , 7 , 0 ) Z ( 3 , 5 , 1 ) = Z ( 5 , 1 , 3 ) Z ( 4 , 3 , 2 ) = 3 6 = 5 0 4 = 1 2 6 0 The most probable distribution ( n 1 , n 2 , n 3 ) = ( 4 , 3 , 2 ) thus accounts for 55% of all possible microstates.
If we assume a Boltzmann distribution, the occupation numbers results ⇒ n i = N ∑ i = 1 3 e − E i / k T e − E i / k T = 9 ∑ i = 1 3 e − i / 3 e − i / 3 ( n 1 , n 2 , n 3 ) ≈ ( 4 . 0 4 , 2 . 8 9 , 2 . 0 7 ) which comes close to the distribution ( n 1 , n 2 , n 3 ) = ( 4 , 3 , 2 ) . The Boltzmann distribution correspond to the most probable energy distribution for a given internal energy U . For a large number N of particles almost all microstates come close to the Boltzmann distribution.