Engine builder

Classical Mechanics Level 4

In a conventional design 4-stroke internal combustion engine, valves control the inflow of air-fuel mixture and the outflow of exhaust from the cylinder. The valves are held in a normally closed position by a spring, and to open the valve at the appropriate time, a mechanical cam pushes the valve open, thus compressing the spring. To close the valve, the cam lobe rotates away from the valve and the spring force closes the valve.

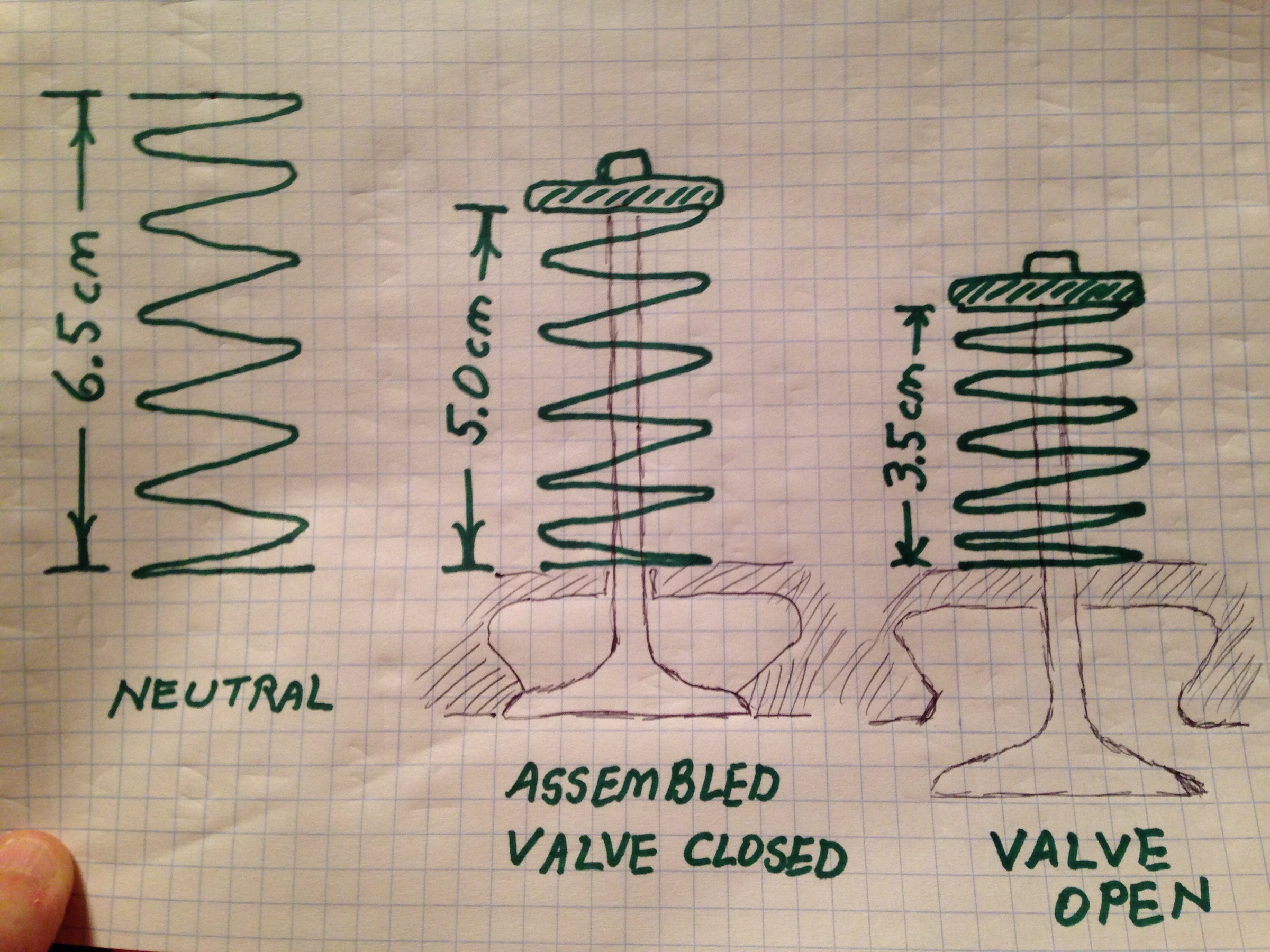
The drawing shows a valve spring. It has a free (neutral) length of 6.5 cm. When the engine valvetrain is assembled, it is compressed to a length of 5.0 cm. This is its assembled length, its length when the valve is closed. (It never gets any longer than 5.0 cm for the life of the engine). At a length of 5.0 cm, it holds the valve closed with a force of 450 NT. When the valve is opened, the spring is compressed to a length of 3.5 cm.

In a 4-stroke engine, each valve opens once each two revolutions of the engine (for example, if the engine crankshaft rotates 10 revolutions, each valve opens 5 times).

An engine has 16 of the valve-valve spring assemblies described above. The engine speed is 6000 revolutions per minute. Find the power required to compress the valve springs in this engine running at this RPM. Express this power in horsepower. Select the closest answer from those on the right.

Details and assumptions:

ignore power required to accelerate a valve or any other moving part
assume spring rebound as valve closes does not contribute back to engine power
1 horsepower = 746 watts
ignore possible effects of friction

14.48 5.33 25.72 17.58 3.62 10.86

1 solution

Matt Owings
Sep 6, 2016

The free length of the spring is 6.5 cm and its length in the assembled engine is 5.0 cm, therefore it was compressed 0.015 meter during the assembly process. At this length (5 cm), the spring exerts a force of 450 NT. We calculate the spring constant k = 450 / 0.015 = 30000 NT/M.

The energy required to compress the spring from 5.0 cm to 3.5 cm is

Strain Energy = 0.5 x 30000 x (0.03^2 - 0.015^2)

Strain Energy = 10.125 Joules.

The engine undergoes 6000 revolutions per minute, or 100 revolutions per second. Therefore, each valve undergoes 50 open-close cycles per second. Each valve spring requires 10.125 x 50 = 506.25 joules/sec. There are 16 valve springs in the engine, so the total power required to open the valves is 506.25 x 16 = 8100 watts. 1 horsepower = 746 watts, so HP = 8100 / 746 = 10.86 HP.

Engine builder

1 solution

0 pending reports