Engineering Geometry #2
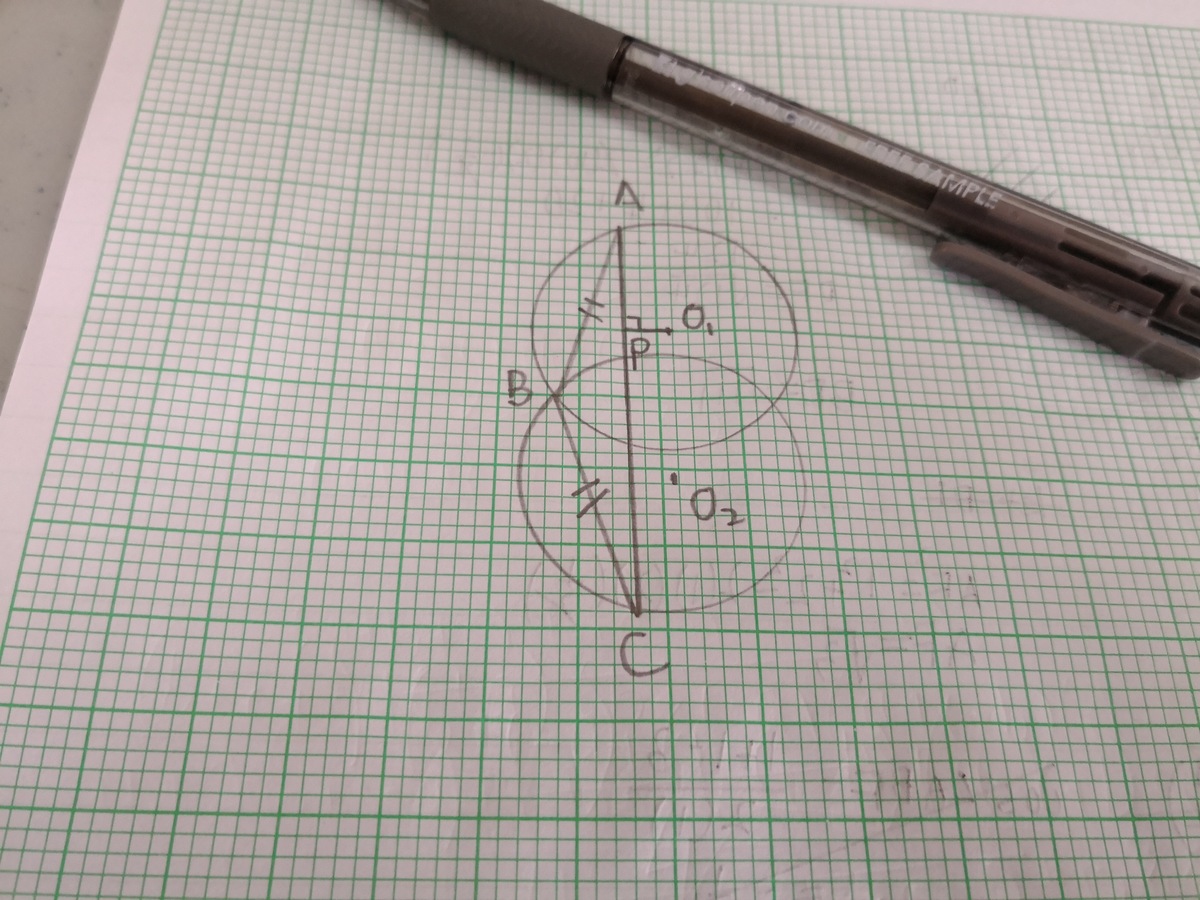 In the image above, given that the circle with center
and the circle with center
are identical with points
and
being reflections of each other on the radical axis of
and
. The radius of the circles
and
. Also,
with
being symmetrical about the radical axis of
and
. We also know that
and
. Upon connecting the centers
and
, the length of the segment
, such that
and
are co-prime positive integers.
In the image above, given that the circle with center
and the circle with center
are identical with points
and
being reflections of each other on the radical axis of
and
. The radius of the circles
and
. Also,
with
being symmetrical about the radical axis of
and
. We also know that
and
. Upon connecting the centers
and
, the length of the segment
, such that
and
are co-prime positive integers.
Compute .
This is part of the set Things Get Harder .
The answer is 697.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
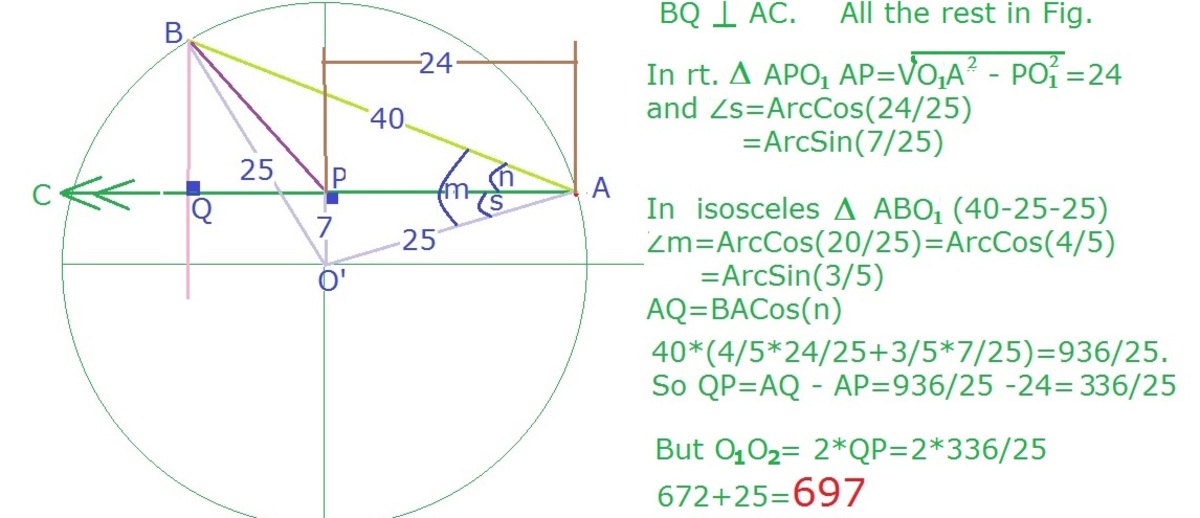
Suppose that O 1 X ⊥ A B ,
Since A O 1 = O 1 B
then A X = X B = 2 0
Also, A O 1 X = X O 1 B
Then, let ∠ A O 1 X = ∠ X O 1 B = θ
s i n θ = 2 5 2 0 = 5 4
c o s 2 θ = 1 − 2 ( s i n θ ) 2 = 1 − 2 ( 5 4 ) 2 = 2 5 − 7 < 0
9 0 ∘ < 2 θ < 1 8 0 ∘
2 θ = 1 8 0 ∘ − cos − 1 2 5 7
Let ∠ A O 1 R = α
sin α = 2 5 7
0 ∘ < α < 9 0 ∘
α = sin − 1 2 5 7
Let ∠ B O 1 Q = β
α + 2 θ + β = 1 8 0 ∘
sin − 1 2 5 7 + 1 8 0 ∘ − cos − 1 2 5 7 + β = 1 8 0 ∘
β = cos − 1 2 5 7 − sin − 1 2 5 7
β = ( cos − 1 2 5 7 + sin − 1 2 5 7 ) − 2 sin − 1 2 5 7
β = 9 0 ∘ − 2 sin − 1 2 5 7
β = 9 0 ∘ − 2 α
cos β = cos ( 9 0 ∘ − 2 α )
cos β = sin 2 α
cos β = 2 sin α cos α
cos β = 2 ( 2 5 7 ) ( 2 5 2 4 )
cos β = 6 2 5 3 3 6
cos β = 2 5 O 1 Q
2 5 O 1 Q = 6 2 5 3 3 6
O 1 Q = 2 5 3 3 6
O 1 O 2 = 2 × 2 5 3 3 6 = 2 5 6 7 2
So, a + b = 6 7 2 + 2 5 = 6 9 7