Enjoy geometry with rectangle, circle and parabola.....

Given that $\begin{cases} x^2 + y^2 = 5 & ...(1) \\ y^2 = \pm 4\sqrt 5 x & ...(2) \end{cases}$ . Substitute $(2)$ in $(1)$ :

$\begin{aligned} x^2 \pm 4\sqrt 5 x & = 5 \\ x^2 \pm 4\sqrt 5 x - 5 & = 0 \end{aligned}$

$\begin{aligned} \implies x & = \pm \frac {4\sqrt 5 \pm \sqrt{80+20}}2 \\ & = \pm (5-2\sqrt 5) & \small \color{#3D99F6} \text{Only 2 acceptable solutions.}\end{aligned}$

Then we have:

$\begin{aligned} x_1 & = \begin{cases} - 5 + 2\sqrt 5 & \implies y_1 = \pm \sqrt{-4\sqrt 5(-5+2\sqrt 5}) & = \pm 2\sqrt{5\sqrt 5-10} \\ 5 - 2\sqrt 5 & \implies y_1 = \pm \sqrt{4\sqrt 5(5-2\sqrt 5}) & = \pm 2\sqrt{5\sqrt 5-10} \end{cases} \end{aligned}$

Area of the rectangle $A = 2\left|x_1\right|\times 2\left|y_1\right| = 4 \left(5-2\sqrt 5\right)\left(2\sqrt{5\sqrt 5-10}\right) \approx \boxed{4.59}$ .

For convenience let $\sqrt5 = a$

we can sea that total required area is $4$ $\times$ (area of gray region).

now find the point of intersection which is in the first quadrant by solving equations $x^{2} + y^{2} = a^{2}$ and $y^{2} = 4ax$ .

we get the point of intersection as $(a(\sqrt5 - 2) , 2a(\sqrt5 - 2)^{1/2})$

therefore the area of gray region $=$ $2a^{2}(\sqrt5 - 2)^{3/2}$ $=$ $1.146$

hence total required area $=$ $4\times 1.146$ $=$ $4.584$

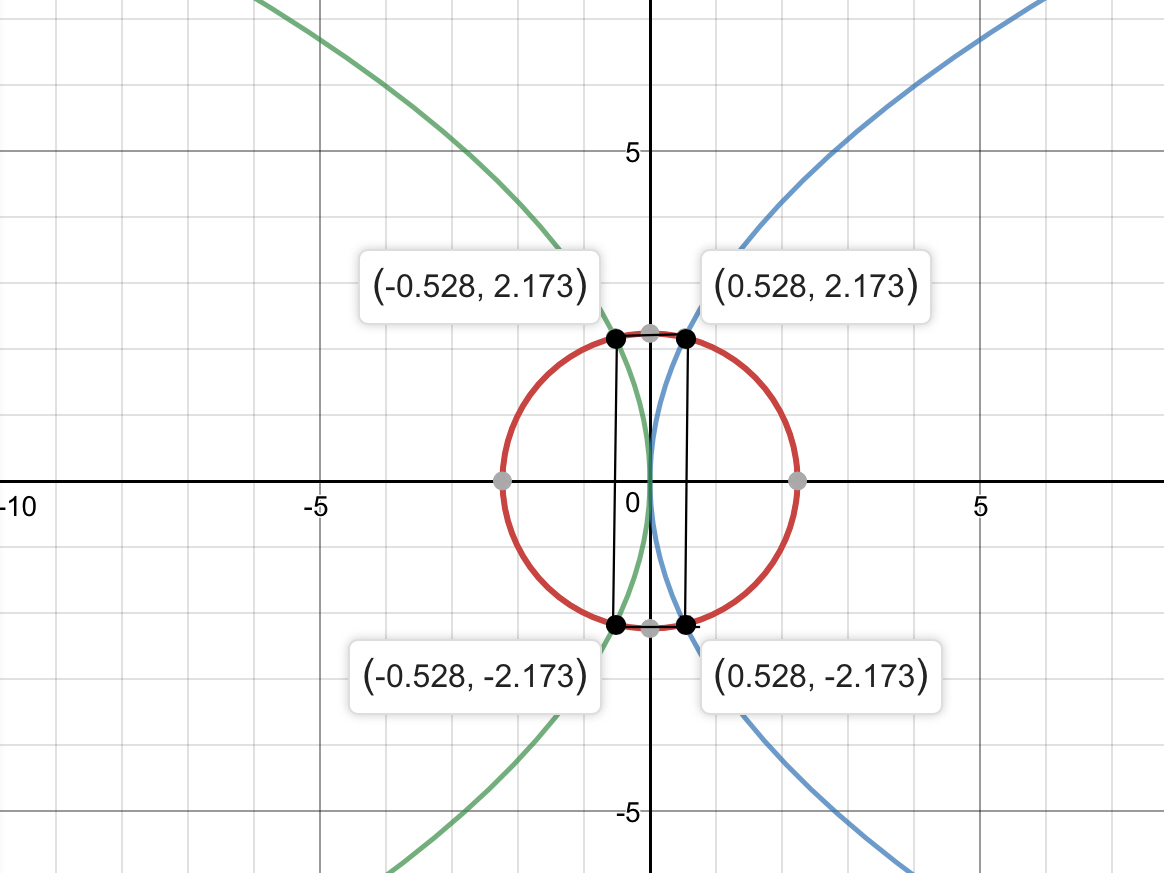We can tell from plotting the graph that the length of the rectangle is: $2.173\times2 =4.346 \text { and the width is } 0.581\times 2= 1.162$ .

Thus, the area of the rectangle is: $4.346\times 1.162= 4.58$ .