Enjoying the View of a Sinusoidal Canyon, Pt. 1
After this problem, you might want to try this problem next.
The rim of a canyon is defined as the curve with (red dotted curve in the image below). A bridge dangles over the canyon at (blue line in the image below).
You start at , trying to enjoy the beautiful view. You are initially able to see all parts of the canyon. However, as you walk along the bridge, you notice that there are points (note that ) where you cannot see all parts of the canyon. Find the minimum possible value of .
Note and Assumptions
- The bridge has zero thickness and is perfectly stationary. Assume that you don't fall off the bridge.
- You are able to see all parts of the canyon if, for any point on , the line segment between you and the point does not intersect any other part of the curve .
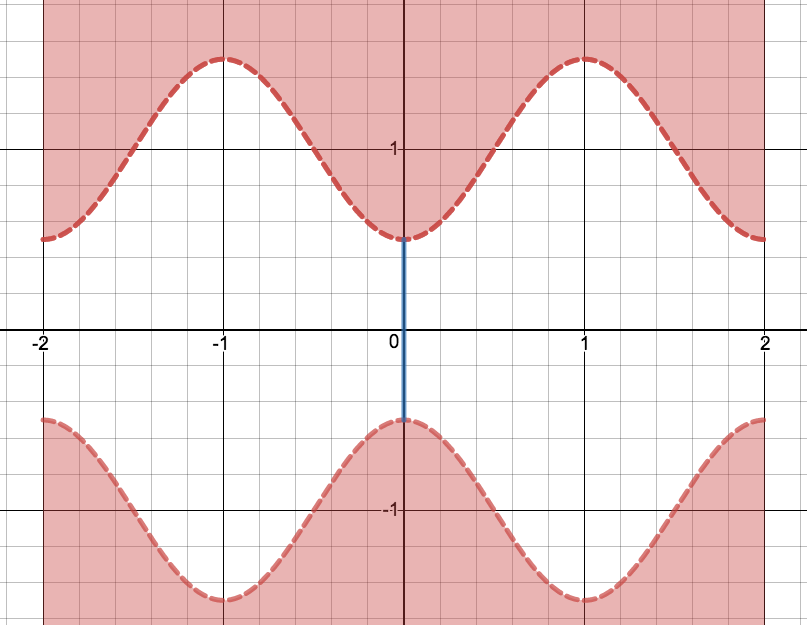 Graph created with Desmos
Graph created with Desmos
Bonus
Now, you rent a helicopter to fly around the canyon. You find that there is a certain area in which it is possible to see all parts of the canyon. How large is the area?
The answer is 0.2146018.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
If there is a tangent line to the rim of the canyon going through your location, and this tangent line is less steep than any other tangent line to the rim, then there will be points on the rim that are invisible to you. Thus as long as you can see the points on the rim with the steepest tangent lines, you will be able to see entire canyon; these points are of course the inflection points of the curve.
We calculate that
f ′ ( x ) f ′ ′ ( x ) = 2 π cos ( π ( x − 2 1 ) ) = − 2 π 2 sin ( π ( x − 2 1 ) )
From your position on the bridge, the important inflection points are the four closest, one in each quadrant; these are easily seen to be ( ± 2 1 , ± 1 ) .
Suppose you are moving upwards and looking to the right. As long as you can see the point ( 2 1 , 1 ) , you can see the rest of the canyon.
The slope of the tangent line at that point is f ′ ( 2 1 ) = 2 π , so the equation of the tangent line is y − 1 = 2 π ( x − 2 1 ) .
The point at which that tangent line crosses the bridge, and thus the highest we can move and still see the whole canyon, is the y-intercept, 1 + 2 π ( 0 − 2 1 ) = 1 − 4 π .
As for the helicopter tour, if we draw all four tangent lines from the points ( ± 2 1 , ± 1 ) , they will border an area in the shape of a rhombus from which you will be able to see the entire canyon; the vertices of this rhombus are the x- and y-intercepts of the tangent lines.
The x-intercept of the previously found tangent line is 2 1 − π 2 , so the area of the rhombus will be 2 ∣ ∣ ∣ ∣ ( 2 1 − π 2 ) ( 1 − 4 π ) ∣ ∣ ∣ ∣ ≈ 0 . 0 5 8 6 3 7 7