Enormous Drawing
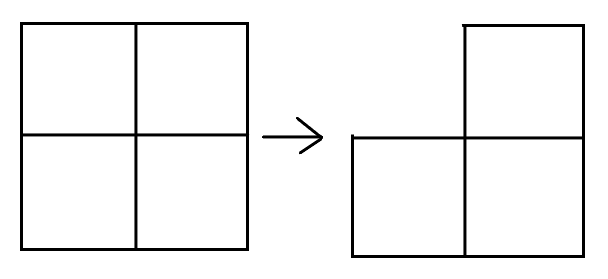
Consider a grid. It is formed with 12 line segments. It is obvious that we cannot draw the grid without lifting the pen nor drawing the same edge more than once.
But if we remove two of the line segments, we will be able to draw it without lifting the pen nor drawing the same edge more than once.
Now consider a grid (made with line segments). How many line segments do I have to remove so I can draw it without lifting the pen nor drawing the same edge more than once?
The answer is 4034.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
After the removal, there must be zero or two points connected by an odd number of lines(“odd points”). In the original grid, there’s 8068 such points. Removing a line segment changes the parity of exactly two points. Therefore the bare minimum should be 2 8 0 6 8 − 2 = 4 0 3 3 line segments. This is, however, impossible, because since there’s an odd number of odd points on each side, all line segments can’t possibly only connect odd points. The construction for 4034 lines simply involves removing 2017 alternating line segments on two neighboring sides and 2016 on the two others, leaving two odd points on opposite sides of the grid.