Enough information?
A circle with radius 217 is inscribed in a right triangle with leg lengths a and b . The circumcircle of this triangle has radius 2017. What is a + b ?
The answer is 4468.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Why is r_i given by this formula?
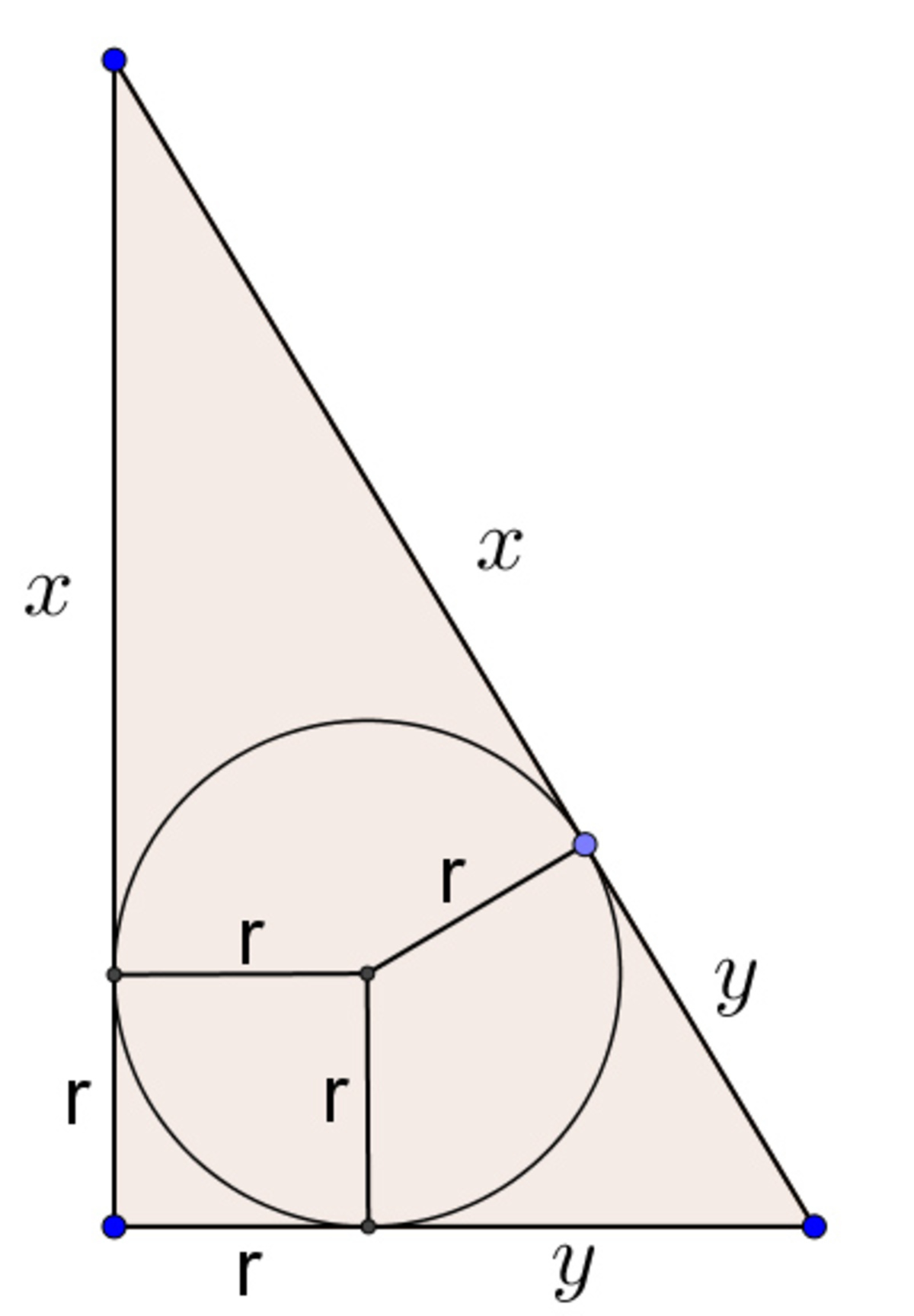
Using Thales' Theorem we get that 2 0 1 7 = 2 x + y . Notice that r = 2 1 7 . From that
a + b = x + y + 2 r = 2 0 1 7 ∗ 2 + 2 1 7 ∗ 2 = 4 4 6 8
Why is the hypotenuse x+y?
Log in to reply
Lol just figured it out it's because of the tangent lines
With the circumcircle's radius r c , we can see that the hypotenuse c of the triangle is 2 × r c = 4 0 3 4 .
Now, the radius r i of the incircle of a right triangle with sides a , b and hypotenuse c is given by r i = 2 a + b − c :
r i ⟹ a + b = 2 a + b − c = 2 r i + c = 2 ⋅ 2 1 7 + 4 0 3 4 = 4 4 6 8