Sharing Candy Fairly

The total number of candies she brings should be divisible by 2,3,4,5,6 and 7. Hence, the minimum number of candies that she should bring is the LCM of those numbers, which is 420.

Take the lowest common multiple of 2, 3, 4, 5, 6 and 7

  =2, 3, 4, 5, 6, 7

(2) = 1, 3, 2, 5, 3, 7

(2) = 1, 3, 1, 5, 3, 7

(3) = 1, 1, 1, 5, 1, 7

(5) = 1, 1, 1, 1, 1, 7

(7) = 1, 1, 1, 1, 1, 1

Thus, LCM = 2 x 2 x 3 x 5 x 7 = 420. This is the least number of candies she must bring

to distribute candies evenly if there are 2, 3, 4, 5, 6, or even 7 top students.let the number of candies be n then n should be divisible by 2, 3, 4, 5, 6, and 7 together.

1) a number is divisible by 5 if we have 0 or 5 in last place

2) a number is divisible by 4 if last two digits of number is divisible by 4 and of-course number should be even

so from conditions 1) and 2) last digit should be 0 only. ( because if last digit is 5 it will not be divisible by even numbers 2,4 and 6)

also if a number is divisible by 6 it must be divisible by 2 and 3

so now minimum requirements are last place of number is 0 and it should be divisible by both 6 and 7 i.e. (6*7=42) so the least number comes is 420 which is divisible by 2, 3, 4, 5, 6, and 7 together.

number is 420

Just finding the common factor 2x2x3x5x7=420

LCM of 2,3,4,5,6,7 will come to 420

Since the number of candies can be divided equally among 2, 3, 4, 5, 6 and 7 people, then the least number of candies required is the lowest common multiple of 2, 3, 4, 5, 6 and 7.

Using algorithm method, I know that the LCM of 2, 3, 4, 5, 6, and 7 is 420 .

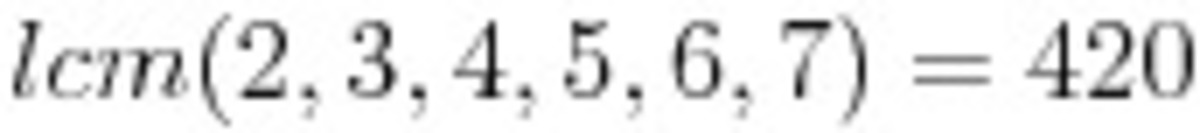
Thus she has to bring at least 420 candies.

420 These are not candies but weed...

The LCM of {2,3,4,5,6,7}= 420

SIMPLY LCM!!!

Find the LCM of 2,3,4,5,6 and 7.

the least number must be divisible by 2,3,4,5,6,7 and the number is 420.

LCM of 2,3,4,5,6,7 is 420

The LCM of the number is required because only 420 candies can be shared equally among 2,3,4,5,6and7 toppers.

I just can't find the logic of one bringing 420 candies...God! To find the answer,you just have to find the LCM of the numbers which is 420.

minimum number of candies she must bring is 420.

because 420 is lowest common number that can be divided evenly if there are 2,3,4,5,6,7 top students.

420 is LCM of 2,3,4,5,6,7.

find the lcm of the given numbers and that will give you the anser

Just find the LCM of the numbers 2,3,4,5,6and7=420 and that's the answer

The number of candies must be divisible by all $n$ in the set of integers from 2 to 7. The smallest number which satisfies this condition is $lcm(2,3,4,5,6,7)$ , which is equivalent to $2 ^2 \times 3 \times 5 \times 7 = \boxed{420}.$

If she brings $x$ candies, $x$ should be divisible by $2,3,4,5,6$ and $7$ to be sure that the candies are equally distributable. Now, the minimum number that is divisible by $2,3,4,5,6,7$ is just $lcm(2,3,4,5,6,7) = \boxed{420}$

2, 3, 4, 5, 6, 7 = 2, 3, 2x2, 5, 2x3, 7 and common multiples = 2x3x2x5x7 = 420 Answer

LCM

simply get LCM of 2,3,4,5,6,7 which is 420

Use the Ladder method, put 2,3,4,5,6,7 and then factorise to get 2^2x3x5x7 as your LCM. Therefore you get 420 which, incidentally, is 420YOLO!!!! (just saying)

L.C.M of 2,3,4,5,,6,7 = 420

It is a very simple problem. Find the Lowest Common Multiple of the numbers Therefore, LCM {2,3,4,5,6,7}=LCM{4,5,6} * 7 Thus, the LCM= the answer=420

The minimum number of candies she should bring is 420.

taking L.C.M of 2,3,4,5,6, and 7;

we get 420.

Therefore, Stella must bring 420 candies to distribute it out evenly.

As written in the question there can be 2, 3, 4, 5, 6, or even 7 top students. So the answer is the L.C.M of the numbers 2,3, 4, 5, 6, 7 which is 420

find the LCM of the numbers

She has to bring multiples of all number of students(2, 3, 4, 5, 6,7) to distribute candies equally. so find the LCM of 2, 3, 4, 5, 6,7 , which is 420.

the ans must be a multiple of 2,3,4,5,6,7

Just simply get the GCF of 2,3,4,5,6 and 7

so the their GCF is 420

For such a kind of problems, find the LCM. And that would be the minimum number needed.

We just need to find the L.C.M of the given numbers ie.420 . That is our answer !!

The minimum number which can be divided equally among 2or3or4or5or6or7 students is the LCM of all those numbers

LCM of 2,3,4,5,6,7 is 420

lcm of all the numbers

She should be able to candies evenly to 2,3,4,5,6 or 7 students, which means we have to find the least no. divisible by 2.3.4.5.6 and 7 which is their L.C.M - 420

find the LCM of 2,3,4,5,6,7= 420

Taken LCM of 2,3,4,5,6,7

I took 2 values like 5 & 6 into consideration. Then multiply them, got 30. Then incremented it by 30 like 30,60,90... and thus found the required value/number.

As it clear that she wont take back any candies if there are 2,3 , 4, 5, 6 or even 7 students who top, it is evident that number of candies that she get is Lowest Common Multiple of 2,3,4,5, 6,7 which is 420 .

LCM - Lowest Common Multiple

Number is LCM of 2, 3, 4, 5, 6, 7 = 420

simply LCM

• The number should be perfectly divisible by 2,3,4,5,6,7,with any number i.e,quotient (no.of candies to each).
• and it should be the first or minimum no. to be divided.
• Hence,L.C.M will provide the required no. .
• L.C.M{2,3,4,5,6,7}= 420 .

lcm is the answer

Simply least common multiple of all numbers

1/2 + 1/3 = 4/6 (take only the value of the denominator) 1/6 + 1/4 = 5/12 (same we did at the first) the idea is to get only the common multiple disregarding the numerator 1/12 + 1/5 = 17/60 do this in repetition until 1/7 1/60 + 1/6 = 11/60 1/60 + 1/7 = 67/420 (420) isolating the denominator we have the least common multiple of every number

For Stella to distribute candies among the students evenly , the number of candies should be divisible by the number o toppers. So the solution will be H.C.F of the number of expected toppers. The H.C.F of 2,3,4,5,6,7 is 420

This requires the lowest common multiple of the possible number of students. LCM(2,3,4,5,6,7)=420

Find LCM of 2, 3, 4, 5, 6 and 7 = 420

Given problem amounts to LCM(2,3,4,5,6,7) LCM(2,3,4,6)=12 LCM(5,7,12)=5x7x12=420 420 is the answer

We know that we can evenly distribute between 2,3,4,5,6,7 kids equally. Hence the number should be divisible by them. We need to find the minimum number so we took Least Common Multiple of 2,3,4,5,6,7 which gave us 420.

Just find their LCM ...