Envelope of Trajectories - 2
A particle of mass 1 k g is projected from the origin with speed u = 2 0 m / s , at angle θ to the horizontal. 0 ∘ ≤ θ ≤ 8 0 ∘
In the range 1 5 ≤ x ≤ 2 5 , there is a force field which applies a force of 1 0 N in the positive Y direction.
Compute the area A bounded by the envelope of all trajectories in the given interval of θ and the X axis. The motion of all trajectories is confined to the X-Y plane. Enter your answer as ⌊ A ⌋ .
Note:
-
An ambient gravitational field acts along the negative Y direction throughout space. Acceleration due to gravity g = 1 0 m / s 2 .
-
⌊ . ⌋ denotes the Floor function
-
This happens to be my 100th problem.
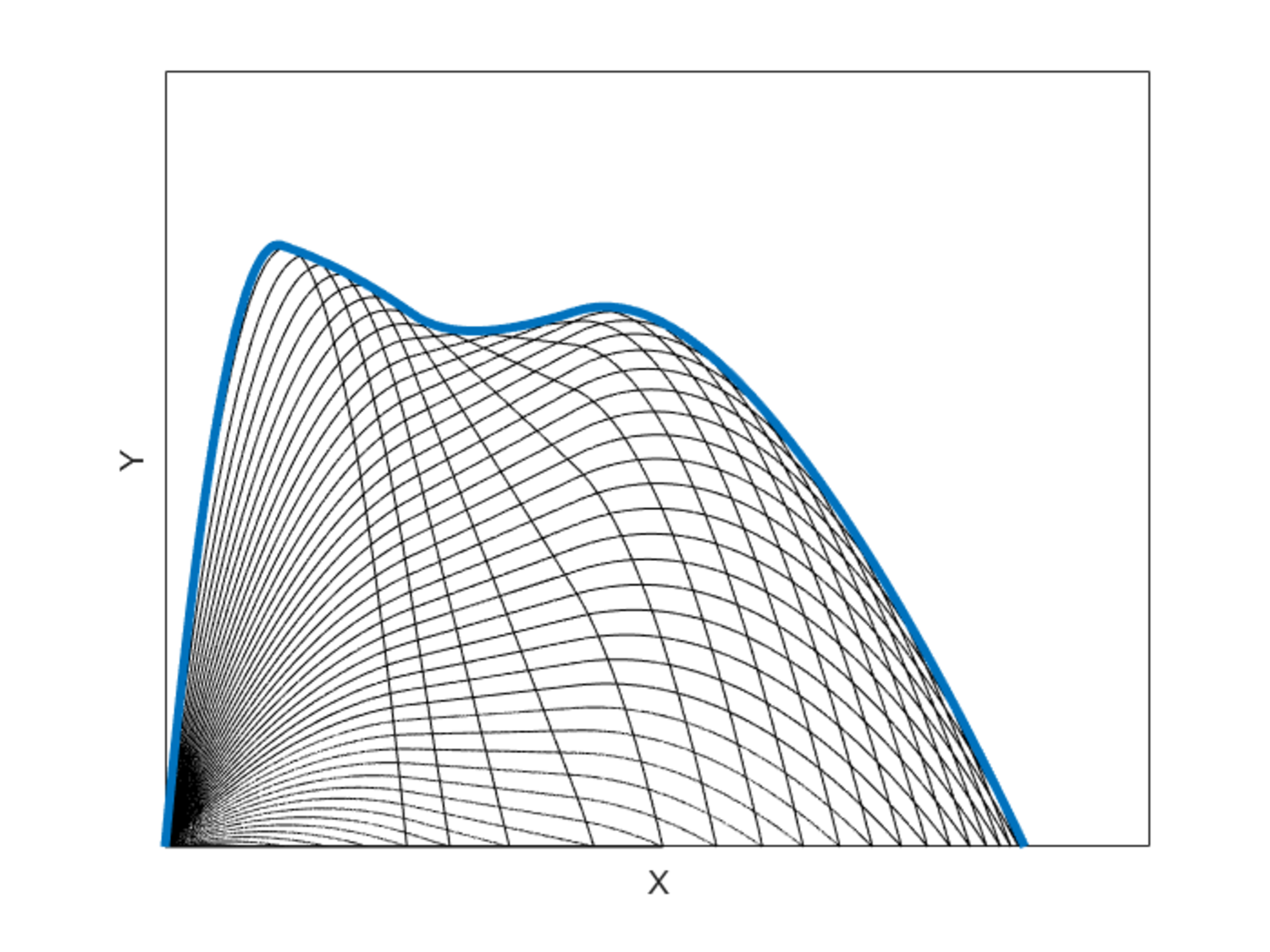
The answer is 717.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thank you for the insightful solution.
This was a fun one. Congrats on the 100 problems. I did a triple sweep, so the computational complexity was huge.
1) Sweep a "measurement x value" ( x m ) over a range in discrete steps.
2) For each x m , sweep the launch angle θ over the allowable range in discrete steps.
3) For each θ , run a time simulation to see the y value when x = x m . If x never reaches x m , that trajectory's y value counts as zero. Store the maximum y value ( y m a x ) for each x m .
4) The incremental area d A = y m a x d x m
In my highest resolution sweep, d x m = 0 . 1 , d θ = 0 . 1 ∘ , and d t = 1 0 − 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 |
|
Thanks for posting. This was a hard one to solve for me as well. I did so by evaluating the closed-form trajectory y as a function of x and the angle of projection θ . Once, I did that, the numerical complexity became manageable as the time advancing Explicit Euler scheme was no longer within the loop. I also see a lot of variability in your results. How did you ensure that your result has converged given the numerical complexity? It must have taken a lot of time.
Log in to reply
I couldn't get the convergence I wanted, because it was too expensive to run the cases. All I could do was get to within an integer or two and then rely on my three tries. Luckily, I got it on the first try.
The initial trajectory is y = x tan θ − 8 0 1 x 2 sec 2 θ and, to begin with, we want to maximize y as θ varies, for 0 ≤ x ≤ 1 5 .
If 0 ≤ x ≤ 4 0 cot 8 0 ∘ , then y is maximized for θ = 8 0 ∘ , so the envelope has equation Y ( x ) = x tan 8 0 ∘ − 8 0 1 x 2 sec 2 8 0 ∘ 0 ≤ x ≤ 4 0 cot 8 0 ∘ If 4 0 cot 8 0 ∘ ≤ x ≤ 1 5 , then y is maximized when tan θ = x 4 0 , and hence Y ( x ) = 2 0 − 8 0 1 x 2 4 0 cot 8 0 ∘ ≤ x ≤ 1 5 Since the initial trajectory has gradient tan θ − 8 3 sec 2 θ at x = 1 5 , in the region 1 5 ≤ x ≤ 2 5 the general trajectory is y = 1 5 tan θ − 1 6 4 5 sec 2 θ + ( x − 1 5 ) ( tan θ − 8 3 sec 2 θ ) and this is maximized when tan θ = 3 ( 2 x − 1 5 ) 8 x , and so the envelope has equation Y ( x ) = 1 6 1 2 5 + 2 4 7 x + 2 x − 1 5 7 5 1 5 ≤ x ≤ 2 5 Finally, in the region x ≥ 2 5 , the general trajectory is y = ( x − 1 0 ) tan θ − 8 0 1 ( x − 1 0 ) 2 sec 2 θ + 1 0 ( tan θ − 8 3 sec 2 θ ) and this is maximized when tan θ = x 2 − 2 0 x + 4 0 0 4 0 x , so the envelope has equation Y ( x ) = x 2 − 2 0 x + 4 0 0 2 0 x 2 − 8 0 1 ( x 2 − 2 0 x + 4 0 0 ) x ≥ 2 5 We deduce that Y ( x ) = 0 when x = 3 0 + 1 0 5 , and so the complete envelope equation is Y ( x ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ x tan 8 0 ∘ − 8 0 1 x 2 sec 2 8 0 ∘ 2 0 − 8 0 1 x 2 1 6 1 2 5 + 2 4 7 x + 2 x − 1 5 7 5 x 2 − 2 0 x + 4 0 0 2 0 x 2 − 8 0 1 ( x 2 − 2 0 x + 4 0 0 ) 0 ≤ x ≤ 4 0 cot 8 0 ∘ 4 0 cot 8 0 ∘ ≤ x ≤ 1 5 1 5 ≤ x ≤ 2 5 2 5 ≤ x ≤ 3 0 + 1 0 5 The area A under this curve can be calculated explicitly, so A = 2 4 2 5 [ 3 4 5 + 8 8 5 + 1 2 8 3 tan − 1 ( 2 1 3 ) − 1 2 8 3 tan − 1 ( 3 2 + 5 ) + 3 6 ln 3 7 + 1 9 2 ln 4 0 0 − 1 9 2 ln 5 2 5 + 1 9 2 ln ( 3 + 5 ) − 2 5 6 tan 1 0 ∘ ] = 2 4 2 5 [ 3 4 5 + 8 8 5 − 1 2 8 3 tan − 1 ( 3 3 1 ( 7 1 5 − 6 3 ) ) + 3 6 ln 3 7 + 1 9 2 ln ( 2 1 1 6 ( 3 + 5 ) ) − 2 5 6 tan 1 0 ∘ ] ≈ 7 1 7 . 5 3 3 1 5 6 1 and hence ⌊ A ⌋ = 7 1 7 .