Envelope of Trajectories
A particle is projected from the origin with speed u = 2 0 m / s , at angle θ to the horizontal. Here, 0 ∘ ≤ θ ≤ 9 0 ∘ .
Compute the area A bounded by the envelope of all trajectories in the given interval of θ , the X axis and the Y axis. The motion of all trajectories is confined to the X-Y plane. The answer is of the form:
A = b a
Where a and b are positive co-prime integers. Enter your answer as a + b
Note: An ambient gravitational field acts along the negative Y direction throughout space. Acceleration due to gravity g = 1 0 m / s 2 .
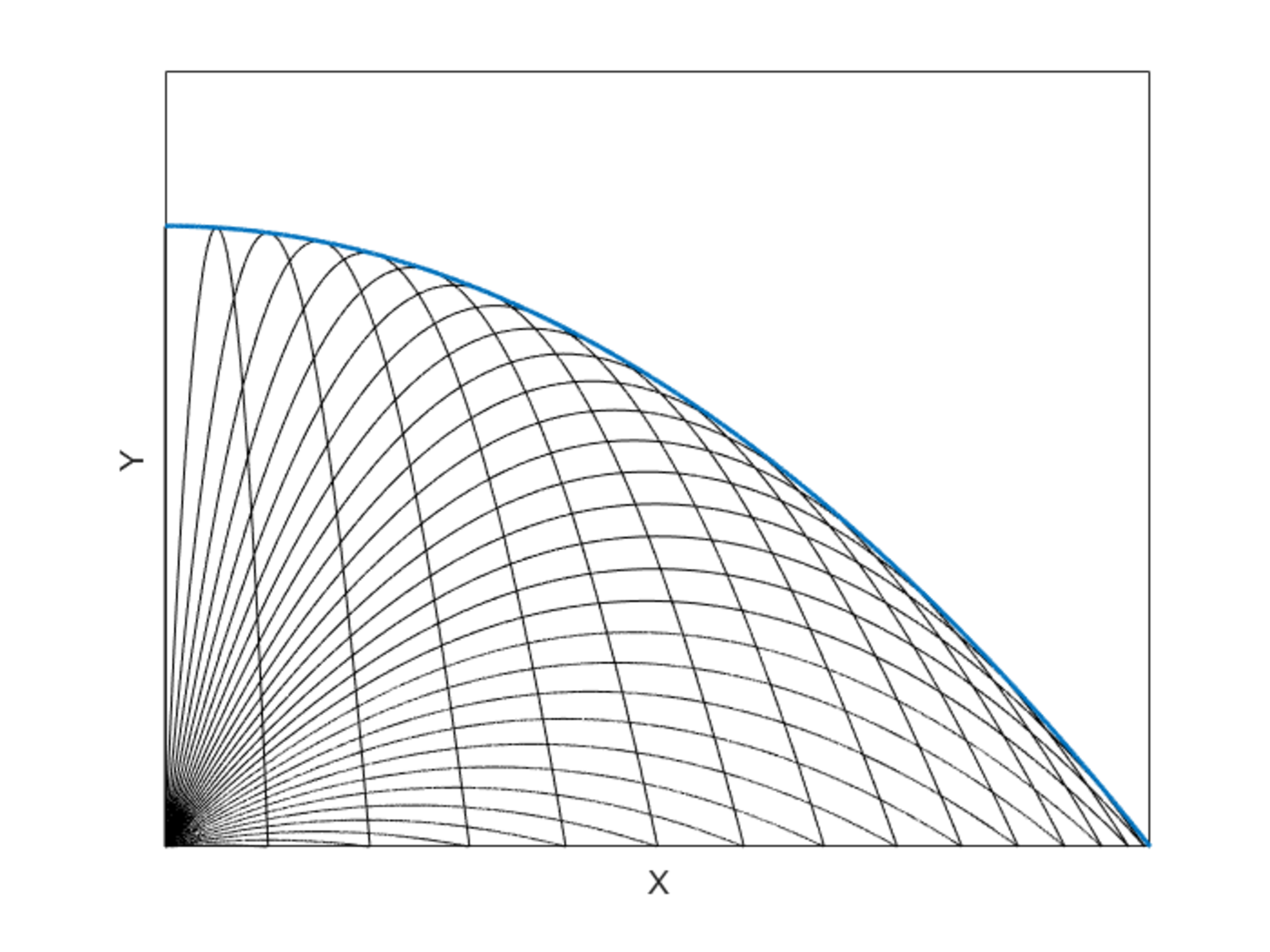
The answer is 1603.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
If you go through the trig to eliminate θ (I multiplied up by cos 2 θ first to make the terms a bit nicer), you get the equation of the envelope to be y = 2 0 − 8 0 x 2
It's really nice that the envelope curve is also a parabola.
Begin by forming the the particles vertical position y as a function of its horizontal position x from the kinematic relationships:
y = v sin ( θ ) t − 2 1 g t 2 Eq1
x = v cos ( θ ) t Eq2
Eliminate the time parameter:
y = tan ( θ ) x − 2 v 2 cos 2 ( θ ) g x 2 Eq3
x = g v 2 sin ( 2 θ ) Eq4
At any given value of horizontal position x , we want to find the launch angle θ that maximizes the vertical height y . We can treat x as a parameter and differentiate Eq3 w.r.t θ .
d θ d y = cos 2 ( θ ) 1 x − v 2 cos 3 ( θ ) g sin ( θ ) x 2 Eq5
Setting the result equal to 0 we find that the tangent of the angle that maximizes the vertical height for a given x to be:
tan ( θ ) = g x v 2 Eq6
Using Trigonometric Identity tan 2 ( θ ) + 1 = cos 2 ( θ ) 1 we find that:
cos 2 ( θ ) 1 = 1 + ( g x v 2 ) 2 Eq7
Now we can substitute Eq6 & Eq7 into Eq3 . This will be the equation of the "envelope" Y ( x ) :
Y ( x ) = 2 g v 2 − 2 v 2 g x 2 Eq8
Now, we are asked for the area bound by the "envelope" Y ( x ) . We are left to determine the limits of integration by finding the maximum possible range x of the projectile. From Eq4 we can differentiate w.r.t θ .
d θ d x = g 2 v 2 cos ( 2 θ ) Eq9
Equating Eq9 to 0 we find:
cos ( 2 θ ) 2 θ θ = 0 ⇕ = 2 π = 4 π
(This is a a well known result )
From Eq4 we have that:
x m a x = g v 2 sin ( 2 4 π ) = g v 2
Finally we integrate Y ( x ) from 0 → x m a x and plug in known values:
0 ∫ x m a x Y ( x ) d x = 2 g v 2 x − 6 v 2 g x 3 ∣ ∣ ∣ ∣ 0 x m a x = 2 g v 2 x m a x − 6 v 2 g x m a x 3 = 3 1 g 2 v 4 = 3 1 6 0 0 m 2
Good problem! I had to think about this for a while. First time actually calculating an "envelope" I believe.
Thanks for sharing your solution. I'm glad you enjoyed solving this one.
This was a fun one. Suppose the particle is launched with speed u at angle θ .
Time at which particle gets to horizontal position x :
x = u cos θ t t = u cos θ x
Vertical position at that same time:
y = u sin θ t − 2 1 g t 2 = x tan θ − 2 u 2 g x 2 s e c 2 θ
Differentiate the y expression with respect to θ and set the resulting expression to zero in order to find the θ value which maximizes y for a given x . The result is:
tan θ = g x u 2
At this point I got lazy. I swept x from 0 to 4 0 , with 4 0 being the horizontal range for θ = π / 4 . For each x , I calculated the optimal θ and the resulting maximum y .
∫ 0 4 0 = y m a x ( x ) d x = 3 1 6 0 0