Epicycloid (Hypercylcoid)
A point on the circumference of a small circle (green) of radius 3 units traces an epicycloid (hypercycloid) (the orange curve) when the small circle rolls without slipping on the big circle (red) which is of radius 1 2 units. Find the total area enclosed by the orange epicycloid. If this area can be expressed as n π , then enter n as your answer.
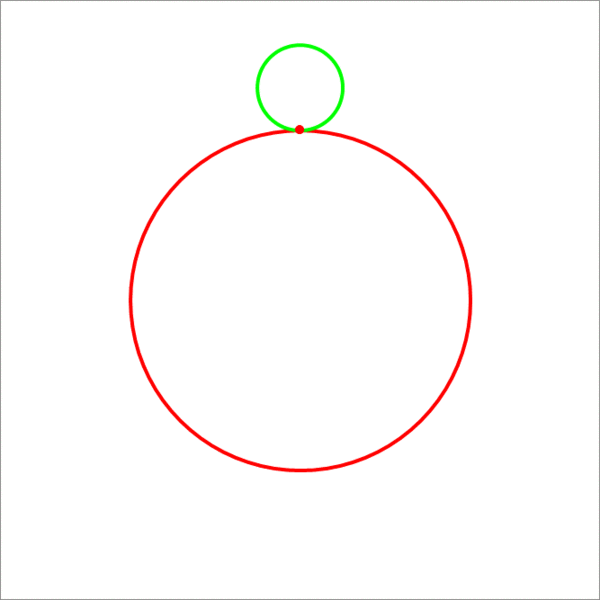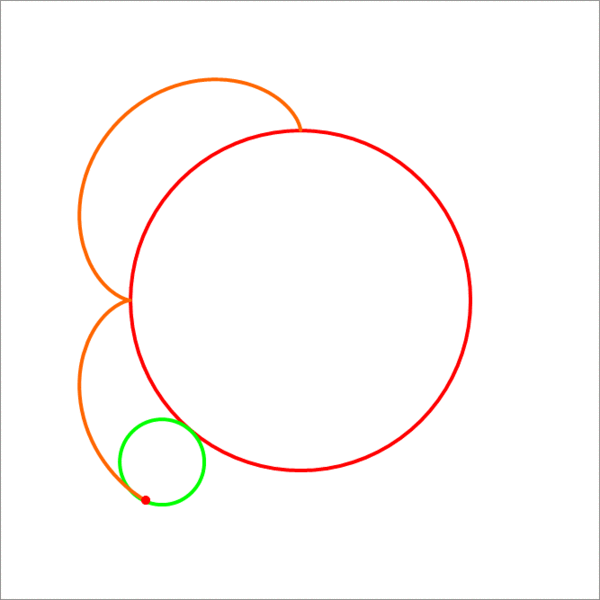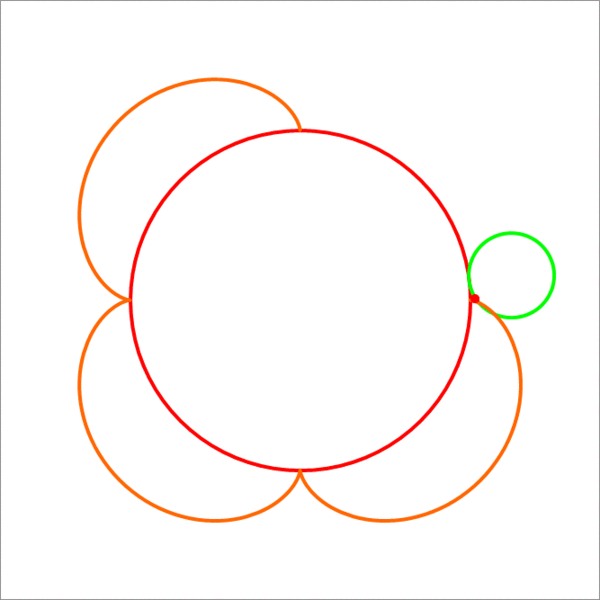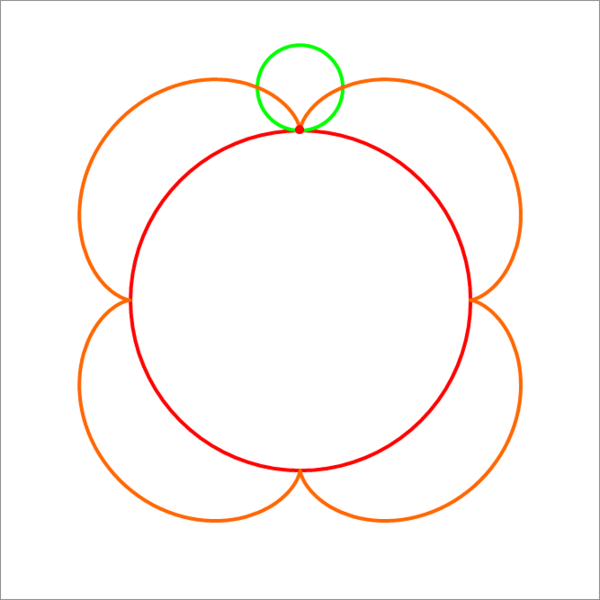
The answer is 270.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Total area under epicycloid = (1+n)
(2+n)
b^2*
π
.
n=ratio of base circle and generating circle radii=12/3=4.
b=gen.circle radius = 3
S
o
(
1
+
n
)
∗
(
2
+
n
)
∗
b
2
∗
=
5
∗
6
∗
3
2
=
2
7
0
The first part of the problem is to find parametric equation of the epicycloid.
Let
P
be a point where the small green circle with radius
r
touches big red circle with radius
R
and let
M
be a point which traces the epicycloid. Introduce two coordinate systems:
S
with origin
O
at center of the big red circles and coordinate axes -
x
and
y
- in horizontal and vertical direction, respectively; and
S
′
with origin
O
′
at the center of the small green circle and one axis always pointing to
O
-
x
′
axis - and the other -
y
′
- rotated
9
0
∘
in anticlockwise direction with respect to
x
′
(we could say that
S
′
rotates around the
S
). Next, angle between positive direction of
x
-axis and vector
O
P
denote with
ϕ
and angle between positive direction of
x
′
-axis and vector
O
′
M
denote with
θ
(see the picture). Since distance traveled by the small circle along the big circle equals the length of the arc subtended by the angle
ϕ
, we have
r
θ
=
R
ϕ
.
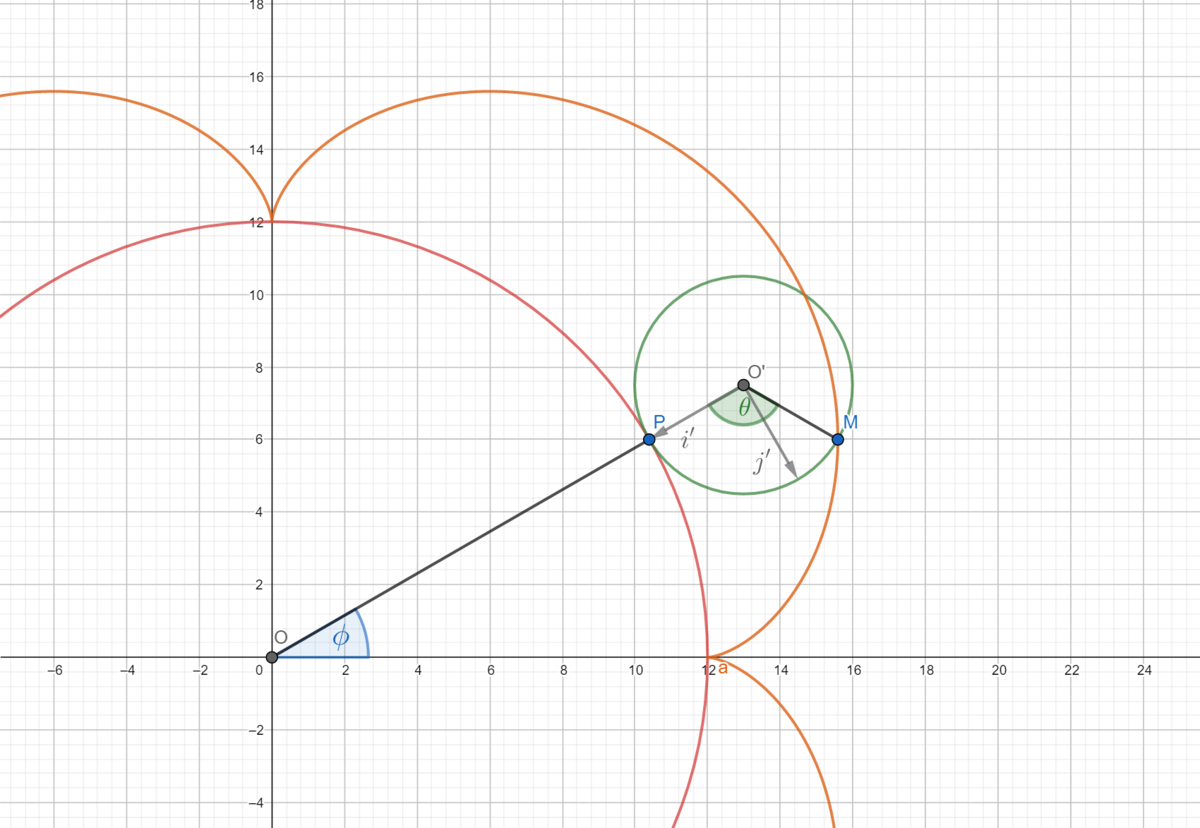 For better presentation of the figure, magnitude of unit vectors
i
′
and
j
′
in the picture is greater than 1.
It follows that the coordinates of origin of
S
′
with respect to
S
are:
x
O
′
y
O
′
=
(
R
+
r
)
cos
ϕ
=
(
R
+
r
)
cos
R
r
θ
=
(
R
+
r
)
sin
ϕ
=
(
R
+
r
)
sin
R
r
θ
,
or equivalently:
O
O
′
=
(
R
+
r
)
cos
(
R
r
θ
)
i
+
(
R
+
r
)
sin
(
R
r
θ
)
j
,
where
i
and
j
are unit vectors in
x
and
y
direction, respectively.
On the other hand, coordinates of point
M
with respect to
S
′
are:
x
M
′
y
M
′
=
r
cos
θ
=
r
sin
θ
,
or equivalently:
O
′
M
=
r
cos
θ
i
′
+
r
sin
θ
j
′
,
where
i
′
and
j
′
are unit vectors in
x
′
and
y
′
direction, respectively.
There are, of course, equations which relate two sets of unit vectors:
i
′
j
′
=
cos
(
1
8
0
∘
+
ϕ
)
i
+
sin
(
1
8
0
∘
+
ϕ
)
j
=
−
cos
ϕ
i
−
sin
ϕ
j
=
cos
(
2
7
0
∘
+
ϕ
)
i
+
sin
(
2
7
0
∘
+
ϕ
)
j
=
sin
ϕ
i
−
cos
ϕ
j
Now, one can easily determine the coordinates of point
M
with respect to
S
by adding vectors
O
O
′
and
O
′
M
:
O
M
x
(
θ
)
=
O
O
′
+
O
′
M
=
(
R
+
r
)
cos
(
R
r
θ
)
i
+
(
R
+
r
)
sin
(
R
r
θ
)
j
+
r
cos
θ
i
′
+
r
sin
θ
j
′
=
(
R
+
r
)
cos
(
R
r
θ
)
i
+
(
R
+
r
)
sin
(
R
r
θ
)
j
+
r
cos
θ
(
−
cos
ϕ
i
−
sin
ϕ
j
)
+
r
sin
θ
(
sin
ϕ
i
−
cos
ϕ
j
)
=
(
(
R
+
r
)
cos
(
R
r
θ
)
−
r
cos
(
R
R
+
r
θ
)
)
i
+
(
(
R
+
r
)
sin
(
R
r
θ
)
−
r
sin
(
R
R
+
r
θ
)
)
j
Thus, we derived the parametric equation for the epicycloid. Notice that we introduced new, more convenient, notation to represent each point as a vector-valued function
x
(
θ
)
, and we assume further on to work only with respect to
S
.
For better presentation of the figure, magnitude of unit vectors
i
′
and
j
′
in the picture is greater than 1.
It follows that the coordinates of origin of
S
′
with respect to
S
are:
x
O
′
y
O
′
=
(
R
+
r
)
cos
ϕ
=
(
R
+
r
)
cos
R
r
θ
=
(
R
+
r
)
sin
ϕ
=
(
R
+
r
)
sin
R
r
θ
,
or equivalently:
O
O
′
=
(
R
+
r
)
cos
(
R
r
θ
)
i
+
(
R
+
r
)
sin
(
R
r
θ
)
j
,
where
i
and
j
are unit vectors in
x
and
y
direction, respectively.
On the other hand, coordinates of point
M
with respect to
S
′
are:
x
M
′
y
M
′
=
r
cos
θ
=
r
sin
θ
,
or equivalently:
O
′
M
=
r
cos
θ
i
′
+
r
sin
θ
j
′
,
where
i
′
and
j
′
are unit vectors in
x
′
and
y
′
direction, respectively.
There are, of course, equations which relate two sets of unit vectors:
i
′
j
′
=
cos
(
1
8
0
∘
+
ϕ
)
i
+
sin
(
1
8
0
∘
+
ϕ
)
j
=
−
cos
ϕ
i
−
sin
ϕ
j
=
cos
(
2
7
0
∘
+
ϕ
)
i
+
sin
(
2
7
0
∘
+
ϕ
)
j
=
sin
ϕ
i
−
cos
ϕ
j
Now, one can easily determine the coordinates of point
M
with respect to
S
by adding vectors
O
O
′
and
O
′
M
:
O
M
x
(
θ
)
=
O
O
′
+
O
′
M
=
(
R
+
r
)
cos
(
R
r
θ
)
i
+
(
R
+
r
)
sin
(
R
r
θ
)
j
+
r
cos
θ
i
′
+
r
sin
θ
j
′
=
(
R
+
r
)
cos
(
R
r
θ
)
i
+
(
R
+
r
)
sin
(
R
r
θ
)
j
+
r
cos
θ
(
−
cos
ϕ
i
−
sin
ϕ
j
)
+
r
sin
θ
(
sin
ϕ
i
−
cos
ϕ
j
)
=
(
(
R
+
r
)
cos
(
R
r
θ
)
−
r
cos
(
R
R
+
r
θ
)
)
i
+
(
(
R
+
r
)
sin
(
R
r
θ
)
−
r
sin
(
R
R
+
r
θ
)
)
j
Thus, we derived the parametric equation for the epicycloid. Notice that we introduced new, more convenient, notation to represent each point as a vector-valued function
x
(
θ
)
, and we assume further on to work only with respect to
S
.
To calculate the enclosed area, we are going to divide it to many infinitesimal triangles with vectors x ( θ ) , x ( θ + d θ ) and x ( θ + d θ ) − x ( θ ) as sides. The area of one infinitesimal triangle is equal to: d A = 2 1 ∥ x ( θ ) × ( x ( θ + d θ ) − x ( θ ) ) ∥ = 2 1 ∥ x ( θ ) × x ′ ( θ ) ∥ d θ = 2 1 ∣ x ( θ ) y ′ ( θ ) − x ′ ( θ ) y ( θ ) ∣ d θ = ( R + r ) 2 R r ( R + 2 r ) ∣ 1 − cos θ ∣ d θ .
Finally, the total area is: A = 2 R r ( R + r ) ( R + 2 r ) ∫ 0 8 π ∣ 1 − cos θ ∣ d θ = 2 R r ( R + r ) ( R + 2 r ) ∫ 0 8 π ( 1 − cos θ ) d θ = R 4 π r ( R + r ) ( R + 2 r )
Replacing R = 1 2 and r = 3 , we get A = 2 7 0 .
Excellent presentation. Thank you for posting your solution.
The parametric equation of the epicycloid is x = 1 5 cos t − 3 cos 5 t y = 1 5 sin t − 3 sin 5 t 0 ≤ t ≤ 2 π and 2 1 ( x ( t ) y ′ ( t ) − x ′ ( t ) y ( t ) ) = 2 7 0 sin 2 2 t after much simplification. The enclosed area is A = ∫ 0 2 π 2 1 ( x ( t ) y ′ ( t ) − x ′ ( t ) y ( t ) ) d t = 2 7 0 π making the answer 2 7 0 .