Equal Angles = Equal Sides?

[This is not a complete solution. It only explains why the second statement is false by providing a counterexample.]

Here is an example of a cyclic hexagon with equal angles, but unequal sides. We can easily verify that all of the angles are $120 ^ \circ$ , and that the 6 points lie on a circle. (What is the radius of the circle?)

Note: You should be familiar with the cyclic quadrilateral case, so it shouldn't be a surprise that equal angles might not imply equal sides.

Hint: This problem is related to when a system of linear equations has a unique solution. In particular, solve for the central angle.

Generalization: Completely classify all cyclic polygons with equal angles.

We will construct a general (cyclic) hexagon that has equal angles, but not equal sides. This shows that the second statement is false.

Let's call the corner points of the hexagon A, B, C, D, E, F, and the center point of the circle M. Draw lines from M to all of the corners, like so:

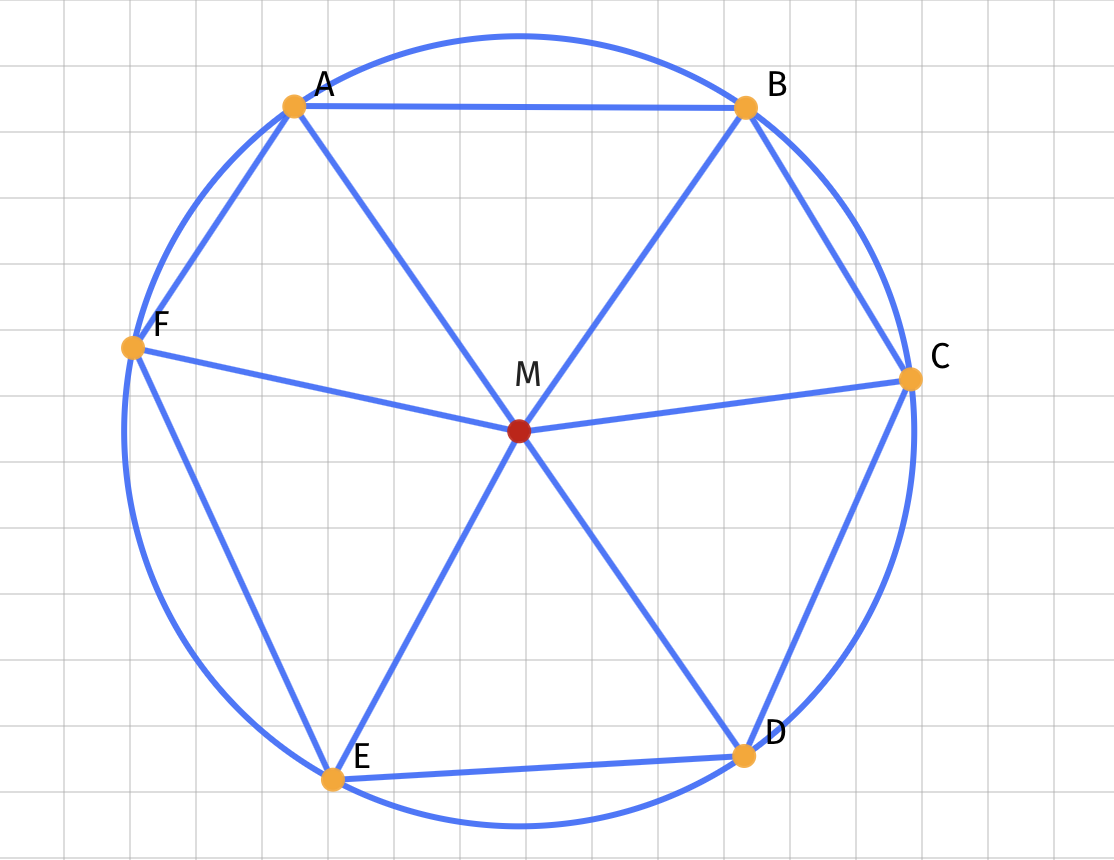
Consider angle A: it consists of two parts, $\angle MAB$ (denoted by x in the picture below) and $\angle MAF$ (denoted by o in the picture below). Note that since $AM = BM$ , also $\angle MAB = \angle MBA$ ( $\triangle ABM$ is an isosceles triangle). We'll mark it with an x as well. Since we're building a hexagon with equal angles, we should mark $\angle MBC$ with an x, so that $\angle A = \angle B$ . We can continue in this fashion to get the following:

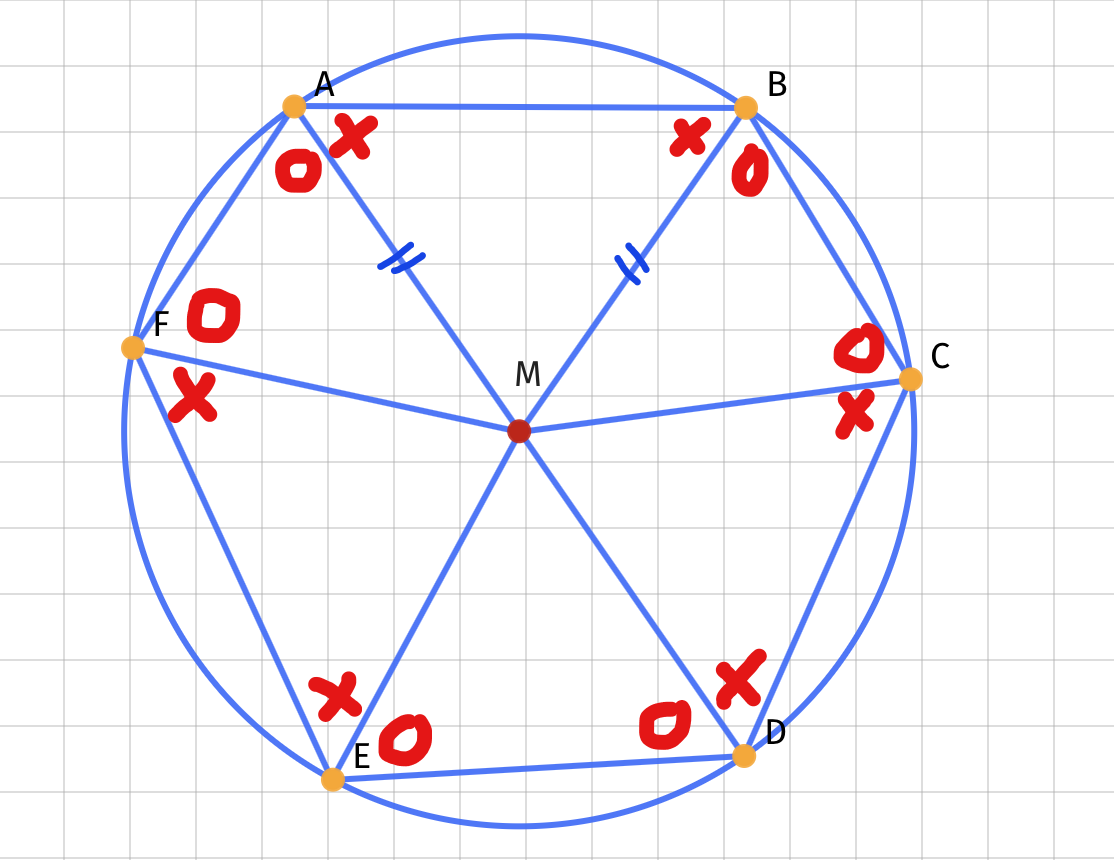
However, we can find multiple angles for x and o (not necessarily equal to each other) such that $6 \times$ (x + o) = $720^{\circ}$ (the sum of the angles of a hexagon). Note that if the x angles and o angles are not equal, the hexagon is not regular: it has three sides of a certain length, while the other three have a different length. (You can see this by noting that increasing x will decrease $\angle AMB$ , which in turn decreases the length of $AB$ .) We have thus found infinitely many examples of a hexagon that has equal angles, but not equal sides.

Using the same construction, you can prove that if a cyclic pentagon has equal angles, then its sides must be equal -- just fill in the x's and o's, and observe that where they meet, there is one point of the pentagon with two x's for its angle (or two o's, depending on what order you filled them in) rather than one x and one o. This necessarily leads to x = o (check for yourself). The other direction (equal sides implies equal angles) is trivial.

This isn't a complete proof for statement number 1, but just a couple hints to get you started. Consider a cyclic pentagon that has all equal angles. Now, draw one of its diagonals.

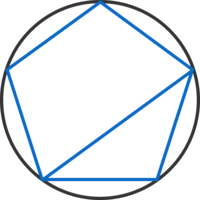
If you can prove that the triangle is isosceles, then you can repeat this process with the other diagonals in the pentagon, and this will prove that all of the sides are congruent. One key fact you will need is that opposite angles in a cyclic quadrilateral are supplementary (they sum to 180 degrees).

To prove the converse, first consider a cyclic pentagon that has all equal sides. Now draw segments connecting each vertex to the center of the circle.

If you can prove that the triangles are congruent, then this will lead to a conclusion that the pentagon is equiangular.