Equal area!
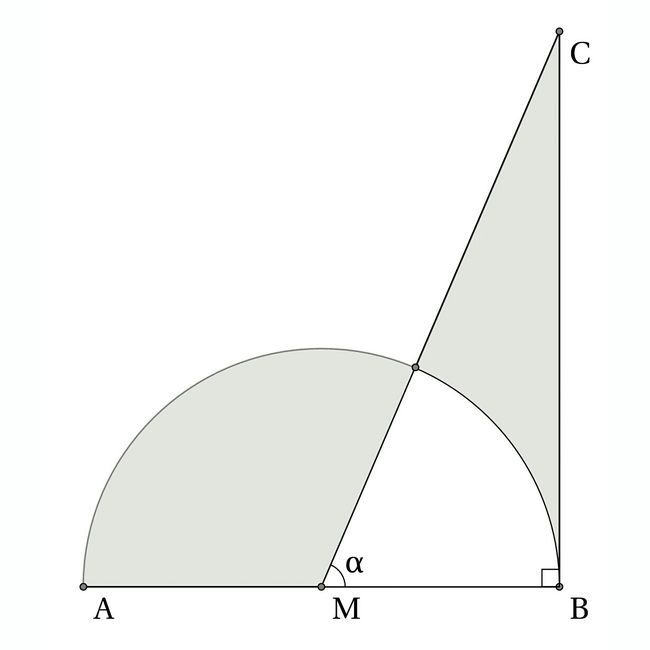 The above figure shows a semicircle with center
M
and a right triangle
M
B
C
. The two shaded regions are equivalent. Find
α
.
The above figure shows a semicircle with center
M
and a right triangle
M
B
C
. The two shaded regions are equivalent. Find
α
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
How is α=arctanπ if π=tanα???
Log in to reply
Technically π = tan ( α ) ⟹ α = arctan ( π ) + n π radians for any integer n , but since we are looking for 0 < α < 2 π radians we take n = 0 to end up with α = arctan ( π ) as the desired angle.
Log in to reply
Thank you for your help Brian. That helped a lot.
because u rma kanu darling aleen!!!
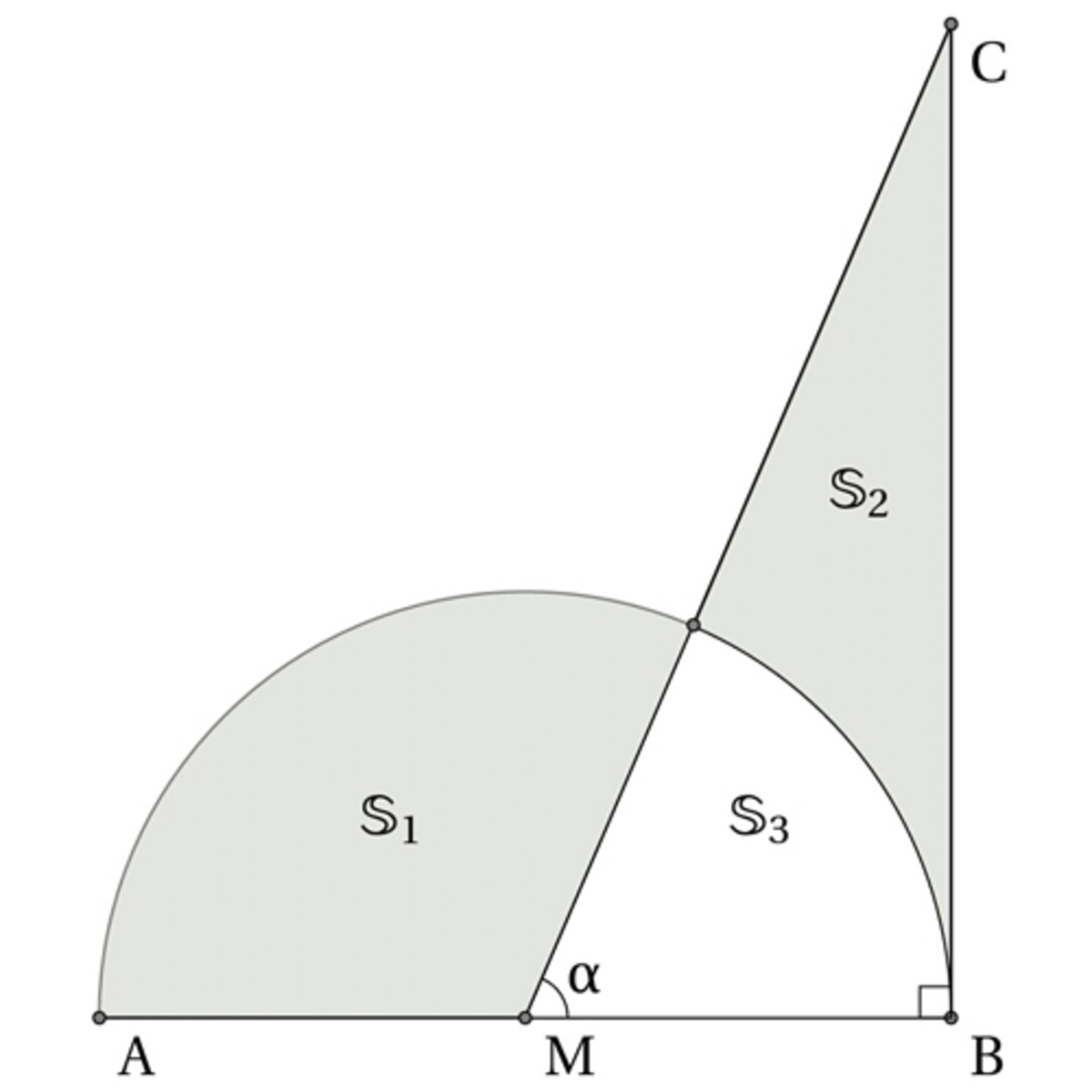
S 1 S 1 + S 3 2 π ⋅ (MB) 2 2 π ⋅ (MB) 2 tan α = π = S 2 = S 2 + S 3 = 2 MB ⋅ BC = 2 MB ⋅ MB ⋅ tan α ⇒ α = arctan π
Given the three options, the answer can only be a r c t a n ( π ) since the domain of both a r c s i n ( x ) and a r c c o s ( x ) is − 1 ≤ x ≤ 1 , of which π is not an element.
That was my logic too
Among the 3 options, only arctan π is real value. Not only to guess, we can find α as follows:
Area of sector = 2 1 r 2 θ
Let height of triangle be h and with r = 1 as we only need to find an angle,
2 1 ( π − α ) = 2 1 h − 2 1 α .
⟹ h = π = t a n α
⟹ α = arctan π
Answer: arctan π
If the two shaded regions have same area also the triangle and the semicircle have same area.
- Area of the semicircle = pi * r *r * 1/2
- Area of the triangle = r * (r * tan alfa) * 1/2
tan (alfa) = pi ,
alfa = arctan (pi)
Simple analysis, since the range of sine and cosine functions are from -1 to 1, and that pi takes the value greater than 1, then it would be obvious that the angle formed would be the inverse tangent of pi (based on the choices :D).. :D
How do you all "type" those equations?
ohoo by seeing BP
tana=(BC)/r if r is the circle radius.then(BC)=r(tana) The area of the triangle MBC is:(1/2)r(BC)=(1/2)r^2(tana). The area of the semicircle is:(1/2)πr^2 Therefore:(1/2)r^2(tana)=(1/2)πr^2 and tana=π therefore a=arctanπ.
In general, the area of a sector of a circle of radius r subtended by a central angle of θ , (in radian measure), is 2 1 r 2 θ . So with ∣ A M ∣ = r the area of the shaded sector with "base" A M is 2 1 r 2 ( π − α ) .
Next, triangle Δ M B C has a base length of ∣ M B ∣ = r and height ∣ B C ∣ = ∣ M B ∣ tan ( α ) = r tan ( α ) . The area of the shaded region of the triangle is then the area of Δ M B C minus that of the circular sector subtended by the angle α . This area is then
2 1 ∣ M B ∣ ∣ B C ∣ − 2 1 ∣ M B ∣ 2 α = 2 1 r 2 tan ( α ) − 2 1 r 2 α = 2 1 r 2 ( tan ( α ) − α ) .
For the two shaded regions to then have equal area, we then require that
2 1 r 2 ( π − α ) = 2 1 r 2 ( tan ( α ) − α ) ⟹ π = tan ( α ) ⟹ α = arctan ( π ) .