Equal areas in decreasing boundaries

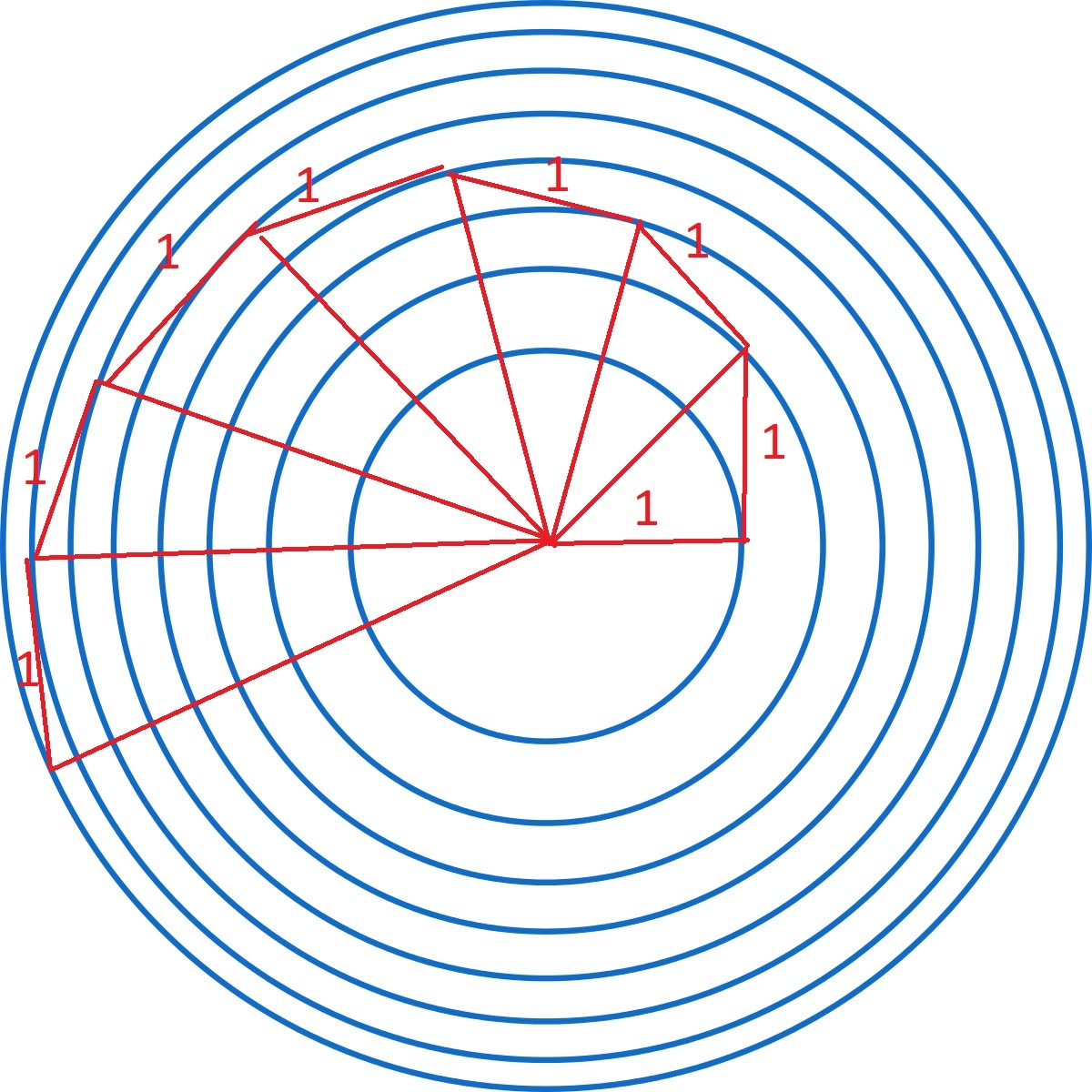
The progression may be defined recursively by $r_{n+1}^2 = r_n^2 + a,$ making the squares of the radii an arithmetic progression. However, the radii themselves do not fit any of the given progressions. Explicitly, $r_{n+1} = \sqrt{r_n^2 + a}.$

Radii of these 8 circles are: sqr(1), sqr(2), sqr(3), sqr(4), sqr(5), sqr(6), sqr(7), sqr(8). So the answer is none of the above.