Equal circular sections

Geometry Level 3

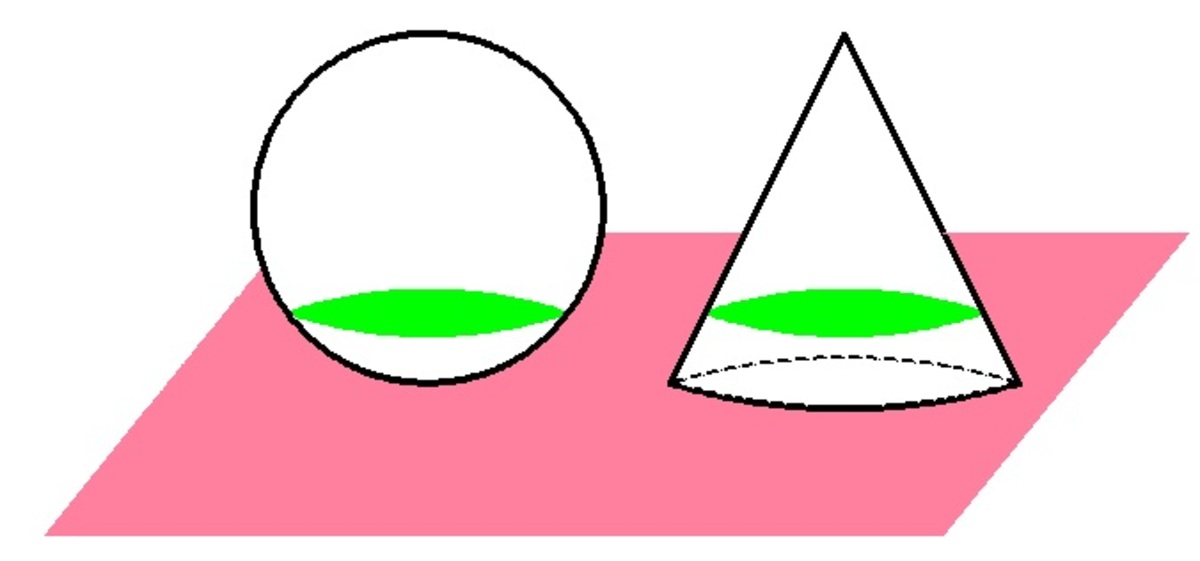A sphere of radius 5 cm and a right circular cone of radius 5 cm and height of 10 cm stand on a horizontal plane as shown in the figure. How far (in cm) from the base of the cone must a cutting plane (parallel to the base of the cone) pass in order to cut the solid in equal circular sections?


The answer is 2.

A Former Brilliant Member by A Former Brilliant Member

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Considering the cone

By ratio and proportion:

10 5 = 10 − y r \frac{10}{5}=\frac{10-y}{r} ⟹ \implies r = 5 − 0.5 y r=5-0.5y ( 1 ) (1)

Considering the sphere

By pythagorean theorem,

r 2 = 5 5 − ( 5 − y ) 2 r^2=5^5-(5-y)^2 ( 2 ) (2)

Substitute ( 1 ) (1) in ( 2 ) (2) ,

( 5 − 0.5 y ) 2 = 25 − ( 25 − 10 y + y 2 ) (5-0.5y)^2=25-(25-10y+y^2)

y = 2 c m \boxed{y=2~cm}

y = 10 c m y=10~cm (absurd)

1 Helpful 0 Interesting 0 Brilliant 0 Confused

The solution y = 10 c m y=10cm is correct in that the circles have an equal radius. It just happens to be zero.

Marta Reece - 4 years, 1 month ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...