This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
If these triangles are in fact equal, then we can assume the bases and hypotenuses are equal to each other.
First find x by setting the bases equal to each other. Subtract 4 from each side. x + 1 x = 4 = 5 Then use your result from x to solve for y and set the hypotenuses equal to each other. Solve for y by subtracting y and 2 from each side. 4 + y 4 2 = 2 y + 2 = y + 2 = y
Since the areas are equal, we have
2 1 ( h ) ( x + 1 ) = 2 1 ( h ) ( 5 )
x + 1 = 5
x = 4
We observed that the bases are also equal, so the triangles are congruent. So
x + y = 2 y + 2
4 + y = 2 y + 2
4 − 2 = 2 y − y
2 = y
Note: In my solution, I assumed that the bases are not equal. But if we look further, we can see that the bases are equal.
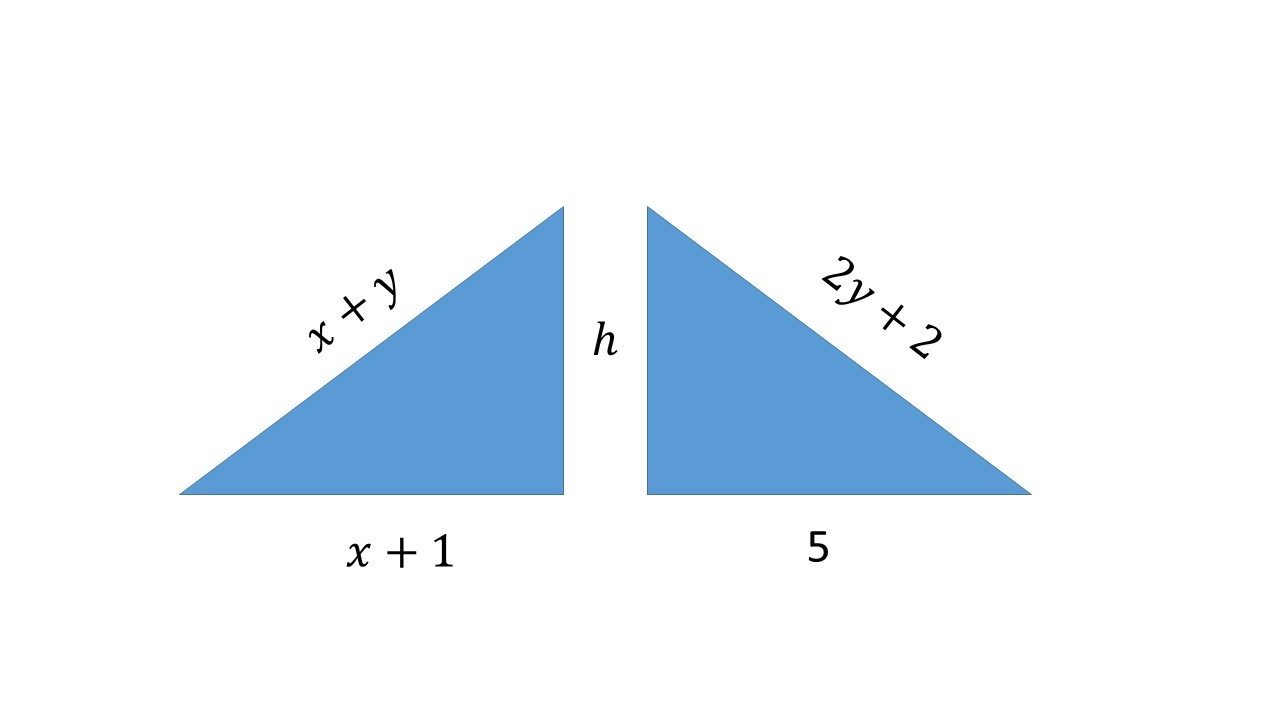
As the areas are same........................................ 1/2×(x+1)×h =1/2×5×h On solving we get x=4. As base of both the triangles are same, the hypotenuese of both triangles will be equal...... Therefore, (x+y)=(2y+2) Substitute x=4 and on simplification we get y=2.