Equilradii Triangle
Geometry
Level
1
Three circles with equal radii form an equilateral triangle whose vertices are the circles' centers.
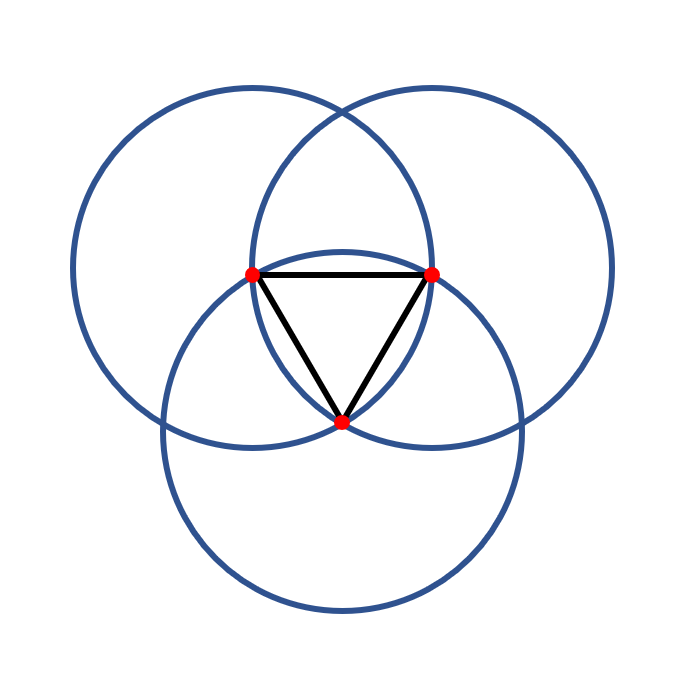In terms of radius, what is the triangle's area?
1/(√3π) r^2
(√3)/4 r^2
(√2)/2 r^2
π/6 r^2
1/2 r^2
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Draw a height in the triangle. Since it's equilateral, the height is also a median, so we get two right triangles with edges of r, 1/2r and h.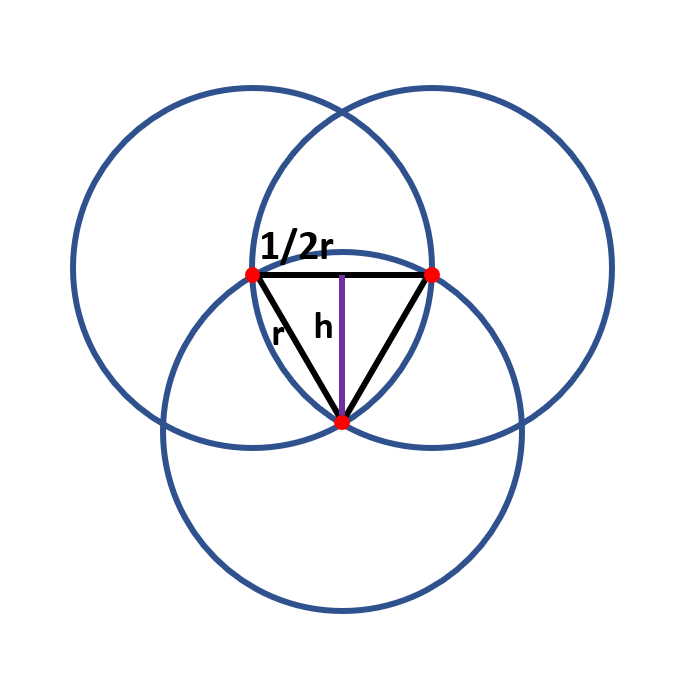
With a little help from the Pythagorean theorem we get the equation:
h^2+(1/2 r)^2=r^2
We solve for h:
h^2=r^2-1/4 r^2
h=√(3/4 r^2)
h=√(3/4) r
Now we can substitute h with √(3/4) r, and by using the formula for the area of a triangle we can solve the problem:
Area of triangle = [√(3/4)r*r]/2
Area of triangle = [√(3/4)r^2]/2
Area of triangle = [√(3/4)r^2][√(1/4)]
Area of triangle = (√3)/4 r^2