Equation of Ellipse
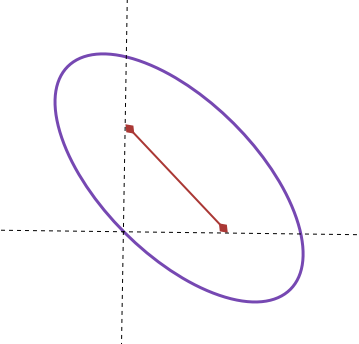 There is an ellipse with focal points
There is an ellipse with focal points
P = ( 4 , 2 )
and
Q = ( 2 , 4 )
One of the points on the ellipse is ( 2 , 2 ) . If the equation for this ellipse is
a x 2 + b x y + c y 2 + d x + e y + f = 0
where g cd ( a , b , c , d , e , f ) = 1 find the maximum value of the following expression:
a + b + c + d + e + f
The answer is 24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Sharky Kesa , question is good, but i think you will want to give that g c d ( a , b , c , d , e , f ) = 1 ,
Because when you ask the maximum value, it can be ∞ !!
Because call the equation as f ( x ) = 0 , then the equation of the ellipse can be written as
k f ( x ) = 0 , where k ∈ r e a l , so you should satisfy that a , b , c , d , e , f are integers, and their gcd is 1.
Log in to reply
Agree I too want to notify about this. He forgot to give g c d ( a , b , c , d , e , f ) = 1
LOL, easy question is a Level 5 question.
Log in to reply
Agree with you.
Maybe because not many people know how equation of a ellipse is derived.... or maybe they gave wrong attempts, increasing the rating !
one of my questions, the 7th part of the set Mistakes give rise to Problems , when initially shared, had got level 5, 190 points. But then, as many as 1 4 0 0 + people tried the question, with near about 400 solvers, so due to those sooo many wrong attempts, it's points had increased to 3 1 5 ... LOL, moderators had to reduce it later.... @Sharky Kesa
found a, b, c but did't knew about equation of rotated ellipse
Log in to reply
Man you can make the equation the ellipse if you know how to write perpendicular distances from a line.
I immediately simplified this for the answer: ( x − 4 ) 2 + ( y − 2 ) 2 + ( x − 2 ) 2 + ( y − 4 ) 2 = 4 Its really tedious though.
We Can Define Ellipse In A Bit Different Way.
The Locus Of A Point Which moves such that the sum of its distances from
two fixed points(the focii) always remains constant which is equal to the
length of major axis .
Now the point (2,2) lies on the ellipse therefore finding the sum of its
distances from focii we get the sum equal to 4 .
let (x,y) be any point on the ellipse
Again its Sum of distance from P And Q Will Be Equal To 4 .
Equating the distances and after a bit of some manipulations we get the
required answer
the question says find the maximum value of the following "equation"?? I think it should be "expression". lol :)
Easy question. The trick is to understand the importance of change of co-ordinate axes.
Firstly equation joining PQ is the major axis. Also mid-point of PQ is the centre of the ellipse. The line passing through the centre and perpendicular to the major axis is the minor axis.
So we write Major axis is x + y − 6 = 0 and centre of the ellipse is M=(3,3) and the equation of minor axis is x = y
Now it is given that (2,2) is a point on the ellipse. By little observation note that it lies on the minor axis.
The length of semi-minor axis is b = ( 3 − 2 ) 2 + ( 3 − 2 ) 2 = 2
Also distance of focus from the centre is c = ( 2 − 3 ) 2 + ( 4 − 3 ) 2 = 2
And we know a 2 − b 2 = c 2
Using this we get a = 2 (a=Length of semi-major axis)
Here comes the final thing.We write eqaution of ellipse in standard form in cartesian co-ordinates as :
a 2 x 2 + b 2 y 2 = 1
Now x-co-ordinate is the perpendicular distance from the y-axis and y-co-ordinate is the perpendicular distance from the x-axis.
Following the similar analogy we can write equation of our ellipse as :
a 2 ( P e r p . d i s t a n c e f r o m x − y = 0 ) 2 + b 2 ( P e r p . d i s t a n c e f o r m x + y − 6 = 0 ) 2 = 1
Perpendicular distance from x − y = 0 is = ∣ ∣ ∣ 2 x − y ∣ ∣ ∣
Perpendicular distance from x + y − 6 = 0 is = ∣ ∣ ∣ 2 x + y − 6 ∣ ∣ ∣
Finally we write our equation as :
2 2 ∣ ∣ 2 x − y ∣ ∣ 2 + ( 2 ) 2 ∣ ∣ 2 x + y − 6 ∣ ∣ 2 = 1
After simplifying we get :
3 x 2 + 3 y 2 + 2 x y − 2 4 x − 2 4 y + 6 4 = 0
Finally we get a + b + c + d + e + f = 3 + 3 + 2 − 2 4 − 2 4 + 6 4 = 2 4