Equidistant points on a unit circle (part 2)
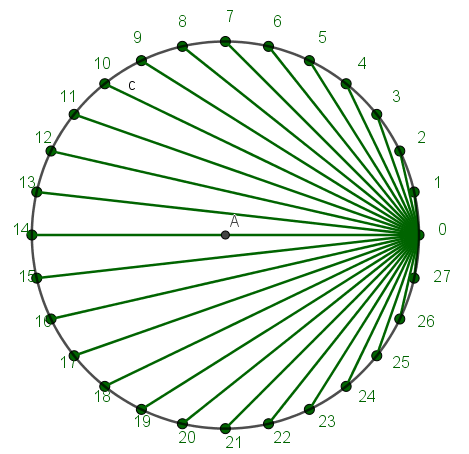
The diagram shows 28 equidistant points (labeled 0,1,2,...,27) placed on a unit circle centered at point A .
Join the point 0 to each of the other points, and let x k denote the length of the segment joining the points 0 and k .
Find the value of ⌊ 1 0 0 k = 1 ∑ 1 4 x k 2 ⌋ .
Notation: ⌊ ⋅ ⌋ denotes the floor function .
The answer is 3000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
k
=
1
∑
1
4
1
0
0
∗
(
X
k
)
2
=
n
=
0
∑
1
3
1
0
0
∗
(
X
n
)
2
=
3
0
0
0
.
Relevant wiki: Cosine Rule (Law of Cosines)
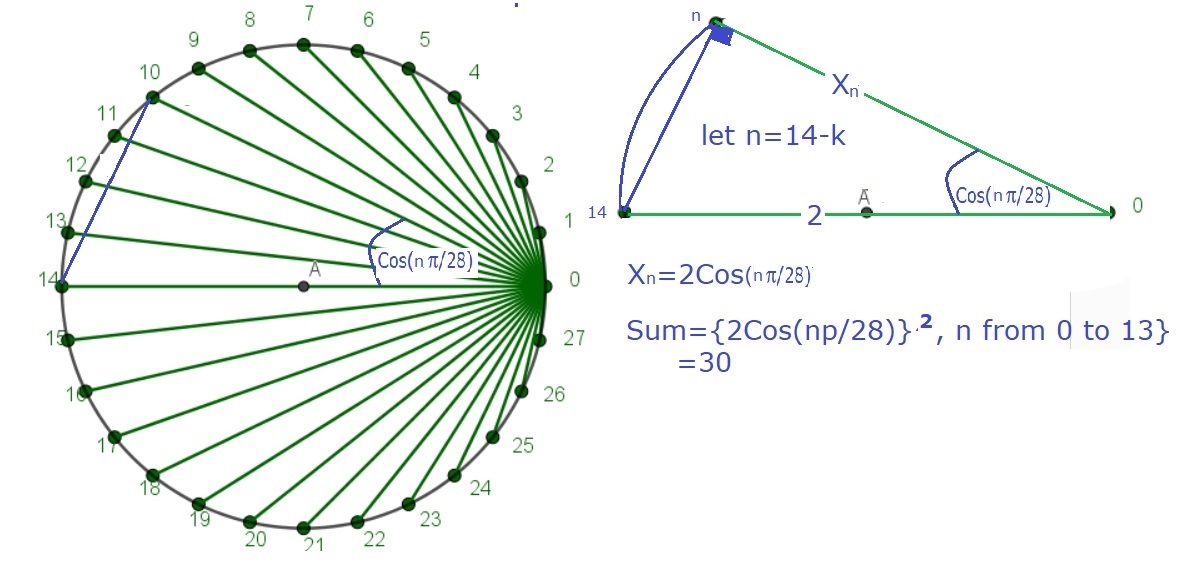
By cosine rule, x k 2 = 1 2 + 1 2 − 2 cos 1 4 k π . Then,
S = k = 1 ∑ 1 4 x k 2 = k = 1 ∑ 1 4 ( 2 − 2 cos 1 4 k π ) = k = 1 ∑ 1 4 2 − 2 k = 1 ∑ 1 4 cos 1 4 k π = 2 8 − 2 ( k = 1 ∑ 6 cos 1 4 k π + cos 1 4 7 π + k = 8 ∑ 1 3 cos 1 4 k π + cos 1 4 1 4 π ) = 2 8 − 2 ( k = 1 ∑ 6 cos 1 4 k π + cos 2 π + k = 1 ∑ 6 cos ( π − 1 4 k π ) + cos π ) = 2 8 − 2 ( k = 1 ∑ 6 cos 1 4 k π + 0 − k = 1 ∑ 6 cos 1 4 k π − 1 ) = 2 8 − 2 ( − 1 ) = 3 0 Note that cos ( π − θ ) = − cos θ
Therefore, ⌊ 1 0 0 S ⌋ = 3 0 0 0 .
Let A = ( 0 , 0 ) and the 28 points on the unit circle, each of these is a roots of x 2 8 = 1 . This means that each point can be represented by a complex number w k = cos 1 4 k π + i sin 1 4 k π , where k = 0 , 1 , 2 , … , 2 7 . The sum of roots is k = 0 ∑ 2 7 w k = 0 .
We may use the idea of vector. Now x k = ∣ 1 − w k ∣ and hence x k 2 = ∣ 1 − w k ∣ 2 = ( 1 − w k ) ⋅ ( 1 − w k ) = ( 1 ⋅ 1 ) − 2 ( 1 ⋅ w k ) + ( w k ⋅ w k ) = 2 − 2 ( 1 ⋅ w k )
Note that k = 0 ∑ 2 7 x k 2 = k = 0 ∑ 2 7 ( 2 − 2 ( 1 ⋅ w k ) ) = 5 6 − 2 ( 1 ⋅ k = 0 ∑ 2 7 w k ) = 5 6
By symmetry, S = k = 1 ∑ 1 3 x k 2 = k = 1 5 ∑ 2 7 x k 2 . It is clear that x 1 4 2 = 2 2 = 4 as x 1 4 is the length of a diameter. Now 5 6 = k = 0 ∑ 2 7 x k 2 = k = 1 ∑ 2 7 x k 2 = ( k = 1 ∑ 1 3 x k 2 ) + x 1 4 2 + ( k = 1 5 ∑ 2 7 x k 2 ) = 2 S + 4 which implies that S = 2 6 .
So k = 1 ∑ 1 4 x k 2 = 2 6 + 4 = 3 0 and hence ⌊ 1 0 0 k = 1 ∑ 1 4 x k 2 ⌋ = 3 0 0 0 .
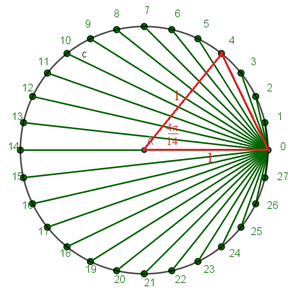
Define y k per the diagram; we have
x k 2 + y k 2 = 2 2
Now note that by symmetry, y k = x 1 4 − k ; this justifies the first line below:
2 k = 0 ∑ 1 4 x k 2 k = 0 ∑ 1 4 x k 2 = k = 0 ∑ 1 4 x k 2 + k = 0 ∑ 1 4 y k 2 = k = 0 ∑ 1 4 ( x k 2 + y k 2 ) = k = 0 ∑ 1 4 4 = 6 0 = 3 0
and since x 0 = 0 , this is in fact the required sum.